Après Osiris, un autre événement de taille nous tombe du ciel, d’un ciel très lointain quoique dans le système solaire : Sedna, en février 2004, a été repéré par des chercheurs américains du California Institut of Technology et de l’Université de Yale.

Découverte aux confins du système solaire, Sedna (une belle déesse des fonds marins chez les Inuits) pose problème aux astronomes. Pas aux astrologues à l’affût d’une caillasse parée d’un nom mythique qui prend un sens en relation avec le climat de son époque d’apparition. Au-delà de Pluton, Sedna doit gouverner le terrorisme international, les recherches sur les secrets de la matière, les problèmes que posent l’euthanasie, le clonage, le mariage des homos… tout ce qui nous plonge dans un abîme de réflexions et, étant donné la révolution de Sedna, près de onze mille ans, on ne sortira pas de sitôt. De plus Sedna, belle déesse en mythologie, est “presque aussi rouge que Mars” en astrométrie ; ce qui, enseigne l’insurpassable Barbault, est significatif de l’agressivité de l’astre, tout comme la couleur jaunâtre de Saturne est significative des cocus et des gagnants du tour de France.

Du côté des astronomes, les abîmes de réflexion tournent autour des données de Sedna qui n’a pas l’air d’être une planète crédible. “Sedna est-elle la dixième planète ?” titre Ciel et Espace, le magazine des marchands du temple d’Uranie.

Dès 1978, il y a de cela un bon quart de siècle, dans le magazine Astrologique (n° 15 de juin 1978), arguant de la cohérence des demi-grands axes de Mercure à Pluton, j’ai déduit, plus que prédit, l’embarras que créerait une 10^e planète :

“Une dixième planète si elle concevable, serait dans la situation d’un arbre loin d’une forêt : il prend peu de sens pour l’écosystème formé par cette forêt. Mercure et Pluton ont déjà des caractéristiques qui rappellent la précarité des conditions aux limites extrêmes, à la frontière des changements d’appartenance. On soupçonne Pluton d’être satellite (évadé) de Neptune. […] Si Pluton a pu s’évader de Neptune sans sortir du système planétaire, que penser du destin d’une autre évasion à une distance deux fois plus lointaine ?”

En fait, ce n’est pas le demi-grand axe de Sedna qui double sensiblement le demi-grand axe de Pluton mais sa distance minimale au Soleil qui est de 76 ou 80 UA (périhélie), tandis que sa distance maximale (aphélie) se situe vers 900 UA. D’où un demi-grand axe de l’ordre de 500 UA, et une période de révolution “d’un peu plus de 10 500 ans”.

Voilà un arbre qui ne cache pas la forêt, qui ne lui fait pas de l’ombre. Dans une famille, telle celle du R.E.T. ou du système solaire (ne pas confondre) il y a toujours des pièces rapportées. L’article (30) cité d’Azar Khalatbari confirme mon analyse de 1978 : Sedna est : “Loin, très loin des trajectoires quasi circulaires des planètes qui font la ronde autour du Soleil.”

Le cœfficient d’excentricité doit être l’un des critères majeurs pour se prononcer quant à l’identification d’une planète. Ce ne peut pas être le seul. Comme en conditionalisme, il faut des critères associés et homogènes pour porter un jugement ou former une hypothèse. Ainsi, pour Emmanuel Lellouch (31) “Sedna annonce peut-être une nouvelle catégorie d’objets”. Selon l’hypothèse personnelle, étayée par les couples d’orbites que donnent les rapports des demi-grands axes, en dehors d’une famille cohérente représentative d’un processus typique de formation, la “nouvelle catégorie d’objets” risque d’être une horde d’astres éjectés, relevant d’un processus atypique, marginal par rapport au processus de formation d’une famille stable. Cette dualisation du système solaire, dans la ligne de la fonction universelle du “duo-duel”, a été consacrée par la dénomination de “planétoïdes” aux astres inclassables. Ces enfants abandonnés, rejetés dans les banlieues nuageuses du système solaire, ressemblent à des enfants normaux, à des planètes, mais les astronomes hésitent à les reconnaître. Sur ce point de droit cosmique, Emmanuel Lellouch répond à Ciel et Espace, le magazine des enragés de l’anti-astrologie :

“Tout le problème est de définir ce qu’est une planète. Si l’on s’en tient à la définition la plus ancienne, ‘tout objet qui tourne autour du Soleil’, alors Sedna n’est pas la dixième planète mais occupe un rang beaucoup plus lointain car on connaît déjà des dizaines de milliers d’astéroïdes ! Si l’on exige qu’une planète ait une forme sphérique ou du moins régulière, Sedna répond sans doute à cette définition. Mais c’est aussi le cas des gros astéroïdes tels que Cérés ou Pallas. Autre possibilité : sont des planètes tous les corps dont la masse dépasse la masse totale des petits objets se trouvant sur des orbites voisines. Dans ce cas, Pluton doit être ‘dégradée’ car la masse totale des objets transneptuniens dépasse la sienne ! Je suggère donc que nous adoptions arbitrairement, et de manière provisoire, une limite en taille [je souligne]. Par exemple, tout corps d’un diamètre supérieur à 2 000 km tournant directement autour du Soleil serait une planète. Pluton ferait toujours partie de la famille, mais pas Sedna… [je souligne]”.

Voilà deux critères, insuffisants en astrologie conditionaliste, qui offrent un thème de dialogue entre conditionalistes et astronomes, si ce dialogue était possible. Pour les symbolistes, ce thème est hors de question : les planètes n’ont pas de dimension, ni d’orbites, et il est vain de faire la différence entre une planète massive et un point vide si tous les deux portent un nom mythologique. Sedna en porte un. Par conséquent elle accède à des éphémérides, publiées sur Internet. Avoir ou non un nom de légende, c’est le critère fondamental de l’astrologie anti-keplerienne.

Les scientifiques vivent dans la chronologie des causes linéaires engendrant des effets linéaires, les conditionalistes dans la globalité, illustrée par le R.E.T., des causes et effets en interactions permanentes. Il a fallu Sedna pour que les linéaires se posent la question “Qu’est-ce qu’une planète ?” Il a fallu un conditionaliste pour poser la même question. Beaucoup plus tôt, en 1980 (Cahiers n° 2) :

Être ou ne pas être du système solaire (extraits)

“…Le problème d’appartenance [au système solaire] n’ayant jamais été vraiment soulevé, l’imprécision ou l’absence de définition permet de qualifier ‘l’étranger’ de ‘familier’ sous prétexte qu’ils relèvent tous deux des lois de la gravitation. […] Finalement, le champ solaire ne définissant pas une dépendance mais une région ouverte, en guise de réfutation de l’astrologie il paraît logique d’avancer que les hautes énergies en provenance des galaxies lointaines doivent être théoriquement plus efficaces que les faibles influences et supposées de nos sœurs planétaires. En d’autres termes : famille, je vous hais. L’argument procède de l’absence de définition d’appartenance. C’est pourquoi je n’ai jamais manqué de dire et de souligner que tout ce qui tourne dans le ciel, naturel ou artificiel, et tout ce qui s’y passe, n’est pas forcément efficace pour l’homme de notre Terre. Les critères d’efficacité [au plan astrologique] peuvent être liés aux critères d’appartenance.” Les influences [astrologiques] efficaces sont le fait de systèmes liés (32).

Nous sommes en 2004. Vingt-cinq ans après, je ne renie pas ce texte. Il concerne une explicative naturelle de l’astrologie qui différencie les systèmes liés, homogènes et cohérents, des formations et évolutions atypiques, mais l’argument ne peut pas intéresser les astronomes. Dommage, la comparaison entre les conditions d’incidences sur le vivant et celles de non-efficience, doit avoir des raisons astrométriques, physiques et biophysiques.

J’ai gardé pour la dégustation une relation numérique entre les distances aux périhélies de Mercure (0,308 UA) et de Sedna. (76 ou 80 UA) :

▶ 0,308 × 76 = 23,408 → 4,84 × 4,84 ou 4,84²
▶ ou 0,308 × 80 = 24,64 → 4,96 × 4,96 ou 4,96²

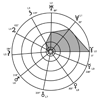
Soit la redondance du périhélie de Jupiter et des couples planétaires. Dans Nombres et Formes du Cosmos (33), je n’ai pas pensé aux produits des distances aux périhélies ; ce nombre apparaît avec le premier angle lié au demi-grand axe de Mercure et avec les distances idéales obtenues après transformation de la figure 1. Pour que l’on comprenne ces distances, je reviens sur sa construction.

Le principe consiste, en partant de Mercure, à prendre comme base et hauteur d’un triangle son demi-grand axe et comme plus grand côté (l’hypoténuse dans un triangle rectangle) le demi-grand axe de Vénus qui devient la base et la hauteur du triangle suivant avec le demi-grand axe de la Terre pour le plus grand côté. On continue jusqu’à Pluton sans négliger l’orbite moyenne des astéroïdes entre Mars et Jupiter. Les neuf triangles consécutifs dessinent une courbe d’allure spirale qui part du Soleil ou d’une distance minimale que j’ai désignée par Alpha = 0,15 UA. Sensiblement le demi-grand axe de Mercure (0,387 UA) élevé au carré.

Les triangles sont définis par trois sommets désignés par leurs angles A, B, C., et par trois côtés opposés aux sommets, désignés par a, b, c. Soit, par convention, a le demi-grand axe de Vénus, et b celui de Mercure. La hauteur relative au sommet B étant égale à b dans ces triangles particuliers, le rapport b/a (l’orbite supérieure divise l’inférieure) correspond au sinus de l’angle C, angle du sommet “solaire”, commun aux neuf triangles. Dans cet exemple, le quotient b/a, (Mercure/Vénus) de 0,387/0,723 égal à 0,535… renvoie, en tant que sinus, à un angle de 32° 36′.

On opère de triangle en triangle en additionnant les angles ‘C’. Des longitudes (élongations) successives apparaissent comme des directions dans l’espace. Après la sommation de 49,77° angle de fin de parcours résultant du rapport Neptune/Pluton, on constate qu’il manque 22,5° (arrondi) pour fermer le cercle. Le sinus de 22,5° est très proche du demi-grand axe de Mercure (0,383 au lieu de 0,387) mais cela entraînerait de poser 0,387/1… ce qui déroge à la procédure des demi-grands axes consécutifs. Un départ à Alpha ? 0,15 UA ferme le cercle. Fermé ou non, le cercle ne change rien aux symétries et à l’organisation de la figure 1 représentative d’une importante caractéristique du système solaire : la bipartition des planètes de part et d’autre de Jupiter. Le schéma en dit plus long que le discours : Pluton à 180° des astéroïdes et proche de Mercure, a perdu les propriétés du versant (partie droite) des planètes gazeuses pour retrouver des airs de famille (densité, taille) avec les planètes telluriques, non gazeuses, du versant gauche.

Le problème de l’ordonnancement des orbites principales est ramené à celui d’une distribution d’angles, de directions dans l’espace qui laissent en suspens un vide (provisoire) de 22,5° pour fermer le cercle. La solution de la répartition des angles est dans les cotangentes des demi-angles des couples de part et d’autre du diamètre déterminé par la position de Pluton et le centre du cercle. Leurs moyennes se calculent, avec un coefficient de proportionnalité, comme on calcule les raies spectrales de l’atome d’hydrogène et les niveaux d’énergie. Dans le cas de cette distribution, les quatre premiers nombres entiers 1, 2, 3, 4, leurs inverses élevés à la deuxième puissance, soit 1/12, 1/22, 1/32, 1/42, conduisent à des résultats d’une précision jamais obtenue dans ce genre de modélisation.

La figure 2 reprend celle publiée dans Pour une astrologie moderne (34) assortie d’un maximum d’efforts pédagogiques avec le soutien du regretté François-Régis Bastide, à qui le conditionalisme doit beaucoup.

FIGURE 2 — Les nombres en haut de la figure indiquent les cotangentes des demi-angles des élongations de la figure 1 obtenues par la sommation de l’angle ‘C’ de chaque triangle. Contrairement à l’algèbre la géométrie est visuelle, de cerveau droit. Plutôt qu’une définition de la cotangente, observez la figure 2. Tout ce que vous devez savoir est que l’angle formé par la position d’une planète sur le cercle, la position de Pluton (360°) et l’axe des x, est le demi-angle de celui formé par la planète, le Soleil (centre de la figure) et Pluton pour la partie droite (planètes lentes) ou l’origine 0°, pour la partie gauche (planètes rapides).

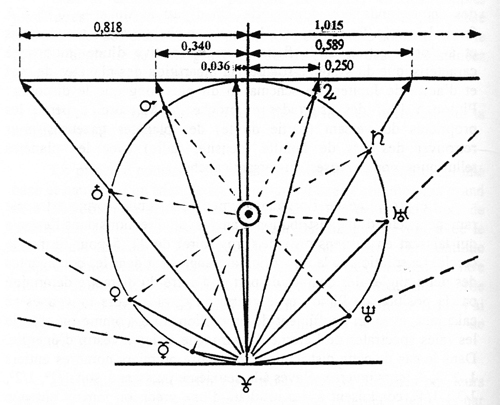
Moyennes des cotangentes des demi-angles :

▶ Jupiter + Cérés (0,250 + 0,036) / 2 = 0,143
▶ Saturne + Mars (0,589 + 0,340) / 2 = 0,465
▶ Uranus + Terre (1,015 + 0,818) / 2 = 0,917
▶ Neptune + Vénus (1,916 + 2,168) / 2 = 2,042

Mercure n’ayant pas de partenaire connu, on note que la cotangente du demi-angle correspondant à sinus 0,387 (son demi-grand axe), soit : 22,8° / 2 = 11,4°… est égal à 4,959. Une réapparition qui n’est peut-être qu’une coïncidence ou qu’une suite à cette mise à jour justifiera. Ce nombre va revenir dans nos angles et distances.

Les moyennes des cotangentes des couples Vénus-Neptune, Terre-Uranus, Mars-Saturne s’obtiennent par la formule :

Racine de : 4,48 × (1/n² − 1/4²) = cotg. du rang ‘n’

en suivant l’ordre de succession :

▶ n = 1 pour Vénus-Neptune,
▶ n = 2 pour Terre-Uranus,
▶ n = 3 pour Mars-Saturne.

Application :

▶ 4,48 × (1/1 − 1/16) = 4,2 v 4,2 = 2,049 au lieu de 2,042
▶ 4,48 × (1/4 − 1/16) = 0,84 v 0,84 = 0,917 au lieu de 0,916
▶ 4,48 × (1/9 − 1/16) = 0,218 v 0,218 = 0,467 au lieu de 0,464

En atomistique vulgarisée par le modèle de Bohr, l’atome d’hydrogène se représente par un noyau et une suite d’orbites. Le premier rayon circulaire, dit rayon de Bohr = 5,29177. 10⁻¹¹ m. Les orbites consécutives multiplient ce nombre par la suite des entiers naturels élevés au carré, soit 22, 32, 42, 52, etc. Ce sont, selon ce modèle, les seules orbites permises. Sur son orbite, l’électron est stable. Il ne se manifeste, ni par émission, ni par absorption d’énergie. Le physicien Georges Gamow enchaîne : “Puisque le postulat de Bohr déclare que le rayon des orbites permises croît comme le carré des nombres entiers consécutifs, il faut conclure, d’après les lois de la mécanique classique (ou de ce qu’il en reste) que l’énergie du mouvement le long de ces orbites décroît d’une orbite à l’autre comme l’inverse du carré des nombres entiers consécutifs.

Poursuivons notre raisonnement : d’après le second postulat de Bohr, un électron n’émet aucun rayonnement le long de son orbite, mais il en émet quand il ‘saute’ d’une orbite à l’autre. Considérons, par exemple, le ‘saut’ d’un électron de la troisième à la seconde orbite. Puisque les énergies correspondantes sont proportionnelles à 1/32 = 1/9 et à 1/22 = 4, l’énergie libérée dans le saut, égale à leur différence, doit être proportionnelle à (1/4 − 1/9).

Si le ‘saut’ se produit entre la 4^e et la seconde orbite, ou entre la 5^e et la seconde, les énergies correspondantes sont proportionnelles à (1/4 − 1/16), (1/4 − 1/25), etc.

Nous arrivons au troisième postulat : il stipule que l’énergie libérée dans un tel saut est directement transformée en un quantum lumineux unique dont l’énergie est, selon l’hypothèse de Planck-Einstein, proportionnelle à sa fréquence (E = hv) ; on en conclut que les fréquences de la lumière émise par un atome d’hydrogène sont proportionnelles à (1/4 − 1/n²), n étant un nombre entier (35) plus grand que 2. Nous retrouvons exactement la mystérieuse ‘formule de Balmer’ relative au spectre de l’hydrogène.”

Peu d’auteurs rappellent que Balmer, découvreur des formules qui donnent les longueurs d’onde des raies de l’hydrogène, était un “pythagoricien clandestin”. À l’intention des lecteurs qui ne sont pas des Mouchassieux ignares, voici un extrait d’un vieux livre : Les secrets de la matière (36) : “Johann Jakob Balmer (1825–1898) professeur à l’université et à l’école de filles de Bâle, posât en 1885 la question de savoir si l’on ne trouverait pas une relation mathématique de ces remarquables séries de raies spectrales. Balmer était un pythagoricien clandestin qui cherchait partout dans la nature et le monde de l’esprit des rapports numériques simples et des proportions harmonieuses [je souligne]. Son mémoire de diplôme sur la géométrie descriptive portait déjà cet étrange titre : Représentation d’ensemble et explication architectonique de la vision du prophète Ezechiel. Il commença par l’élément le plus simple, l’hydrogène.”

J.J. Balmer a réussi une transition révolutionnaire du symbole au signal. Pour un scientifique, peu importe la source, il n’y a que le résultat qui compte ; pour un symboliste peu importe le résultat, le départ est celui d’un symboliste.

Helmut Carl, explique ensuite le rôle des nombres entiers dans les secrets de la matière et notamment dans celui des raies spectrales de l’hydrogène, l’atome le plus simple et le plus répandu. Je dois préciser que le nombre n qui désigne l’orbite, n’est pas le seul nombre caractéristique de son identité atomique, et que lorsqu’on quitte l’atome le plus simple, pour les autres tout se complique. L’appartenance d’une planète au système solaire pourrait donc exiger, en premier lieu, la simplicité des niveaux ‘n’ de l’hydrogène ? D’un point de vue astrophysique, je n’en jurerais pas, mais pour un système biophysique communiquant du non-vivant au vivant pour passer de l’astrométrie à l’astrologie naturelle, cela me paraît évident.

“On connaissait depuis 1866 les longueurs d’onde des quatre premières raies de l’hydrogène par les mesures de l’astronome suédois Angström. Balmer s’en servit pour ses calculs et finit par trouver une relation qui n’était pas moins admirable que la suite pythagoricienne des sons harmoniques supérieurs en musique. Sa loi pour la fréquence v, c’est-à-dire le nombre de vibrations des raies de l’hydrogène, s’écrit aujourd’hui :

▶ v = R (1/2² − 1/n²)

R est une constante, n peut être tout nombre entier à partir de 3. Cette formule remarquable avec les carrés des nombres entiers donne les résultats jusqu’à la cinquième décimale. Elle contient même davantage encore, car si l’on remplace 1/2² par 1/3², la formule rend compte des raies infrarouges de l’hydrogène, que Balmer ne connaissait pas encore, et avec 1/12 on obtient la série des raies ultraviolettes, si bien que l’on peut écrire généralement :

▶ v = R (1/m² − 1/n²)

m et n pouvant être tous les nombres entiers à condition que n soit plus grand que m. En 1898 le Suédois Rydberg montra l’universalité de la constante R, qui, avec des suites un peu plus compliquées de carrés, s’applique aussi à la série de raies spectrales d’autres éléments.” (37)

En résumé. Soit : R, la constante de Rydberg (38), la généralisation de la formule permet d’exprimer et classer les fréquences :

Avec : m = 1 série de Lyman, dans l’ultraviolet

▶ v = R (1/1² − 1/n²) (n = 2, 3, …).

m = 2 série de Balmer dans le visible

▶ v = R (1/2² − 1/n²) (n = 3, 4, …).

Ensuite, trois séries dans l’infrarouge :

Série de Paschen, infrarouge proche, m = 3

▶ v = R (1/3² − 1/n²) (n = 4, 5, …).

Série de Brackett, infrarouge lointain, m = 4

▶ v = R (1/4² − 1/n²) (n = 5,6, …).

Série de Pfund, infrarouge très lointain, m = 5

▶ v = R (1/5² − 1/n²) (n = 6, 7, …).

Les “orbites” atomiques étant surtout des images utiles à la vulgarisation, il est préférable de parler de niveaux d’énergie, de raies d’émission ou d’absorption, de longueurs d’ondes ou de nombre d’ondes. Des constantes physiques relient les niveaux d’énergie aux autres expressions. On ne parle plus de “saut d’une orbite vers une orbite supérieure ou inférieure” mais de “saut quantique”. Enfin, il est convenu d’indiquer les deux nombres entiers concernés par le départ et l’arrivée d’un saut quantique qualifié de transition. Par exemple, la fréquence v correspondant à la transition du niveau 1 à 4 s’écrira :

v 1,4 = R (1/1² − 1/4²)

Les différentes séries de raies spectrales sont définies par le niveau de “retour” de l’électron excité à son état fondamental, état d’équilibre. Ainsi, dans la série de Lyman, le niveau 1 est fondamental, dans la série de Balmer le 2, et dans les suivantes les niveaux 3, 4, 5.

La série des cotangentes planétaires cible le niveau n = 4. Quatrième orbite en langage imagé. Ce peut être un départ (émission), des niveaux 1, 2, 3 vers le niveau 4, qu’une retombée en cascade vers le niveau 4. Nous avons une représentation analogique, sinon une voie d’explicative atomistique de la bipartition du système solaire et de ses symétries indécelables sans la méthode des rapports des demi-grands axes. Notre cerveau, pour fonctionner sur un mode intuitif, a besoin d’images, écrit Stanislas Dehaene dans La Bosse des maths (39). L’approche est intuitive, imagée, mais la précision des calculs serre de près l’image. Il est au moins sûr et avéré que les nombres entiers sont aussi présents et importants dans l’organisation du système solaire, voire la formation des planètes, que dans les niveaux d’énergie de l’atome d’hydrogène et leurs formules de transitions. Reste à savoir s’il n’y a qu’une similitude, deux modèles semblables sans action l’un sur l’autre, ou une relation causale. Dans les deux cas, nos savants feraient mieux d’être un peu plus curieux.

En substituant au coefficient 4,48 (également en relation avec les nombres entiers comme nous le verrons plus loin) un coefficient calculé à partir de 4,48 et des constantes physiques on passe des cotangentes planétaires élevées au carré à l’expression d’une énergie de transition, à celle de sa longueur d’onde, ou de sa fréquence, selon le coefficient et l’intuition que l’on a de la meilleure relation. Inversement, et ce qui est plus intéressant, de quatre niveaux d’énergie (en électronvolt) de transitions, de leurs fréquences, longueurs d’onde, on déduit, par les mêmes coefficients, des cotangentes élevées au carré en relation (trigonométrique) avec huit demi-grands axes planétaires.

Qu’ils s’adressent au grand public ou à des spécialistes, les revues scientifiques font aussi du racolage par des titres tapageurs… mais le fond de l’article est intéressant à connaître pour savoir qui de l’astrologue ou du présumé scientifique mérite la palme de fumiste.

Les physiciens ont recensé un minimum de quatre forces en “action” dans la Nature en attendant de les unifier dans une force unique si une cinquième force, encore inconnue mais soupçonnée, ne vient pas perturber les calculs des théoriciens. Ces forces classiques décelées par l’expérience et l’observation ont des “constantes” mathématiques dont, à part Mouchassieux, on peut se demander si elles n’ont vraiment jamais varié depuis la naissance de l’Univers jusqu’à ces derniers temps. Le pourquoi de ces constantes, de leur dénomination, leurs valeurs et leurs fonctions est expliqué dans Les constantes universelles de Cohen Tannoudji (1). Ce n’est pas l’objet de cet article qui soulève uniquement la question de savoir si les physiciens ont résolu ou réfuté l’hypothèse de Paul Dirac (2), un savant dont Mouchassieux n’a certainement pas tout lu… ou tout compris.

David Larousserie, auteur de l’article de Sciences et Avenir, est mieux informé. Commentant les expériences et les analyses de trois chercheurs australiens, à propos des risques d’erreurs (c’est moi qui souligne) il précise : L’affaire est donc loin d’être close. L’ironie de l’histoire, c’est que les théoriciens n’ont guère été surpris. Voilà près de soixante-dix ans que l’inconstance des constantes est dans l’air du temps. L’un des plus grands, Paul Dirac, avait déjà osé toucher à l’une de ces constantes pour conclure que leur valeur était parfaitement ajustée pour permettre notre existence.

Mouchassieux peut s’accrocher au fait que la variation remonte au Big Bang ou qu’elle est minime, de l’ordre de 0,0007 % “selon les mesures effectuées entre 3,5 et 13 milliards d’années après le Big Bang”. Après le racolage tapageur de la première page, on termine dans la modération : Dans la nature, à chaque force fondamentale est associée une constante dite de couplage qui est un nombre sans dimension, produit et division de certaines de nos constantes familières. Et si l’une de ces constantes fondamentales bouge, alors toutes doivent bouger. Mais, pas trop, car notre histoire depuis le Big Bang est très chatouilleuse. De petites variations sur ces grandeurs et ce sont des conséquences telles que nous ne serions même plus là pour en parler ! Or nous sommes bien là, ce qui est la preuve que ces variations n’ont pas été si importantes et si elles l’ont été, ce fut sans doute lors des premiers babillages de l’Univers. Il reste donc encore beaucoup à apprendre pour comprendre ce qui se cache loin, très loin derrière les virgules. La beauté du monde est sans doute dans ces détails.

Et dans la laideur qui s’affiche chez un Mouchassieux, icône de l’ignorance prétentieusement savante.

Tandis que les années passent l’Histoire ne s’arrête pas en si bon chemin. Dans le numéro de juin 2004, la revue Pour la Science, aux titres moins racoleurs que Sciences et Avenir, j’ai relevé un article qui relance le débat :

Les constantes… le sont

De nouvelles mesures astronomiques indiquent que les constantes universelles n’ont pas varié depuis dix milliards d’années.

L’article expose par quelles méthodes ingénieuses les astrophysiciens — ceux-là ne sont pas d’Australie — ont constaté ou déduit que l’une des constantes chères à la Physique n’avait pas “diminué de plus de quelques cent-millièmes au cours des dix milliards d’années passés”. Un temps qui dépasse largement celui des réincarnations successives pour devenir un brillant physicien. Il est question, dans le même article d’autres constantes, mais pas de la constante ‘G’ de la gravitation.

Grâce à ces dix milliards d’années Mouchassieux aurait-il raison de flétrir l’astrologue qui n’a que quelques réincarnations derrière lui pour excuser son manque d’ouverture aux galaxies ? D’âme récente, je ne m’intéresse qu’à la fanfare de mon village et qu’au système solaire. De là mon manque d’humilité.

Cependant Mouchassieux n’a pas le dernier mot. Dans le même numéro, un autre article, L’Univers avant le Big Bang remet en cause le concept de commencement. Le Big Bang n’est pas comme on le croit avec des réincarnations naïves, le début de l’Univers, il existe une théorie dite des “cordes” (vibrantes comme celles d’un violon) susceptibles d’unifier toutes les forces. Et dans les avantages de cette théorie, pas tellement originale par rapport au vieux modèle du “tout est vibrations”, il ressort que (c’est moi qui souligne) : “…les constantes qui décrivent l’intensité des forces fondamentales, telle la constante de gravitation ou la charge électrique, ne sont plus fixées arbitrairement, mais apparaissent dans la théorie des cordes sous forme de champs dont les valeurs évoluent au cours du temps. […] Au cours de différentes époques cosmolo-giques, les ‘constantes’ de la physique ont ainsi pu connaître de minuscules variations. Les astrophysiciens cherchent aujourd’hui à les mesurer en observant l’Univers lointain.”

En science les principes font autorité. Une constante qui varie ou a varié n’est plus une constante mais une constante variable selon les époques, si stable soit-elle de nos jours. C’est ce qu’avait compris Paul Dirac.

Il y a une morale à cette histoire : lorsqu’un scientifique ou présumé tel s’adresse à un astrologue ou présumé tel, le scientifique est irrésistiblement attiré par le trou noir de sa bêtise. Une constante. Prudence conditionaliste : je ne crois pas que la bêtise soit une constante universelle. Elle varie selon les époques, les individus et les corporations. À notre époque, les astrologues et les scientistes sont des champions.

Le savantissime rationaliste Georges Charpak, pourfendeur de sorcières aux côtés d’Henri Broch qui marche sur le feu mais pas sur les eaux, a déclaré que l’on pouvait être intelligent et avoir des neurones débiles, réservés à la parapsychologie et l’astrologie. A-t-il appliqué ce superbe raisonnement à son cas d’anti-astrologue ?

Notes :

▶ 1. Les constantes universelles. Gilles Cohen Tannoudji. Hachette. 1991.
▶ 2. “Paul Adrien Maurice Dirac. Physicien britannique (1902–1984). […] Il est l’auteur de l’équation qui porte son nom et qui constitue la description la plus générale de l’électron, tenant compte pour la première fois simultanément de la mécanique quantique, de la relativité et du spin. Il déduisit de cette équation l’existence de l’anti-électron (positon) et donc de l’antimatière (1927)…” Extrait du Dictionnaire illustré des noms propres (Le Petit Robert. 1995).

Article paru dans le n° 29 des Cahiers conditionalistes (4^e trimestre 2004).

  Article suivant — Varuna et la bêtise astrologique