Demi-grands axes et gravités
Les périodes Tg sont supposées liées à une situation originelle d’oscillations ou translations. Ceci ne veut pas dire que l’absence de corps célestes aux distances correspondantes les prive de toute efficacité astrologique. Les rapports √(L / g), contemporains, organisés comme le modèle R.E.T. font la preuve du contraire. Au plan astrométrique, qui ne se dissocie pas de l’astrologie naturelle, l’ordre de grandeur des périodes obtenues par 2π√(L / g), entre 2 et 360 jours, est celui des étoiles pulsantes, des satellites, d’astres qui graviteraient entre la Terre et le Soleil. Enfin, elles sont voisines des 25 jours de rotation équatoriale du Soleil. Mars, au centre, n’a que 18 jours. Il est possible de le déplacer, avec l’ensemble des distances dg, pour recentrer le tout sur la durée de rotation solaire. Suivant les règles de la mécanique céleste, ce déplacement s’opère par un apport de vitesse2 supplémentaire. À toutes les vitesses Vg2 du tableau XXV on ajoute un supplément de 63,252 soit 4000 km2/s2 (en négligeant 0,57 km2/s2). Les nouvelles distances, désignées par d3, pour les distinguer de dg, s’obtiennent en divisant 2 ⋅ G ⋅ M3 par Vg2 + 63,252. En unités UA, il est commode de remplacer 2 ⋅ G ⋅ M3 par 2 ⋅ V2 de la Terre, soit 2 fois 29,7852 = 1774 km2/s2.

De d3 à la puissance 2/3, vient T3, en années, puis en jours avec le produit T3 × 365,25 j.
TABLEAU XXVIII — Application de la formule pour le calcul de d3, T3, ω3, f3 des planètes et Soleil U.
| Planète |
Vg
(km/s) |
√(Vg2 + 4000)
(km/s) |
d3
(UA) |
T3
(jours) |
ω3
(°/jour) |
f3
(cm/s2) |
| Soleil |
134,9 |
149 |
0,080 |
8,2 |
43,6 |
92,2 |
| Vénus |
106,2 |
123,6 |
0,116 |
14,5 |
24,9 |
43,8 |
| Mercure |
101,9 |
119,9 |
0,123 |
15,8 |
22,8 |
39,2 |
| |
| Jupiter |
91,7 |
111,4 |
0,144 |
19,7 |
18,3 |
28,9 |
| Mars |
81,2 |
103 |
0,167 |
25 |
14,4 |
21,1 |
| Saturne |
72,3 |
96 |
0,192 |
30,8 |
11,7 |
16 |
| |
| Uranus |
61,9 |
88,5 |
0,227 |
39,4 |
9,1 |
11,5 |
| Neptune |
59,5 |
86,8 |
0,235 |
41,7 |
8,6 |
10,7 |
| Pluton |
35,5 |
72,5 |
0,337 |
71,6 |
5 |
5,2 |
| |
| Lune |
204 |
214 |
0,039 |
2,8 |
129 |
390 |
| Terre |
102,4 |
120,4 |
0,123 |
15,7 |
23 |
39,4 |
| Cérés |
48,1 |
79,5 |
0,280 |
54,4 |
6,6 |
7,5 |
Après ce déplacement dans les règles, les moyennes géométriques des couples R.E.T. donnent sensiblement la vitesse, distance, période, force centrale de Mars, et, par conséquent, pour la période et la vitesse angulaire, les 25 jours de rotation équatoriale du Soleil actuel et sa vitesse angulaire journalière de 14°,4 (moyenne).
À la surface, cette rotation est différentielle, variable selon la latitude : 25 jours à l’équateur, 37 jours au pôle. Que deviennent les périodes inférieures à 25 j ? Les calculs ci-dessus remontent à 1982. Depuis, il y a du nouveau sur le Soleil : “Les résultats recueillis à ce jour indiquent que la vitesse de rotation diminue légèrement en partant de la surface, jusqu’à environ le tiers du rayon : une observation qui va à l’encontre des idées habituelles. Plus près du centre, au contraire, la vitesse de rotation augmente : de 25 jours à la surface, la période passe à 15 jours.” [1]
Il y aurait, au tiers du rayon, une zone frontalière départageant les vitesses et les périodes : inférieures à 25 j vers le centre, supérieures vers la surface.
Calculons nos tiers. Le Soleil U est à 0,08 UA et Pluton à 0,337. Écart : 0,337 − 0,08 = 0,257. Le tiers de 0,257 = 0,086. Ajoutons-le à la distance du Soleil U, et nous trouvons : 0,08 + 0,086 = 0,166 UA, position médiane de Mars. Pluton se place évidemment 2/3 plus loin de Mars : 0,166 + (2 × 0,086) = 0,338.
TABLEAU XXIX — Moyennes géométriques des couples planétaires avec Soleil U pour Pluton, et les données de Mars comme constantes.
| Couple |
√(d3 × d′3)
(UA) |
√(ω3 × ω′3)
(°/jour) |
√(T3 × T′3)
(jours) |
√(f3 × f′3)
(cm/s2) |
| Soleil - Pluton |
0,164 |
14,8 |
24,3 |
21,9 |
| Vénus - Neptune |
0,165 |
14,67 |
24,54 |
21,65 |
| Mercure - Uranus |
0,167 |
14,42 |
24,96 |
21,17 |
| Jupiter - Saturne |
0,166 |
14,6 |
24,65 |
21,52 |
| Mars |
0,167 |
14,4 |
25 |
21,1 |
Ce retour à la source solaire affine la précision, mais les cas particuliers comme ceux des planètes doubles (Terre-Lune, Pluton-Charon) et les résultats identiques pour Terre et Mercure restent à éclaircir.
En dernière colonne : moyenne géométrique de la force centrale. À la distance 0,1676 UA la chute seconde par seconde ou le creux de l’espace-temps est de 21 cm/s2. Comme indiqué en 1re partie, des causes différentes peuvent conjuguer leurs effets. Lorsqu’il ne s’agit pas d’accélération, mais de longueur, 21 cm, c’est aussi une raie “interdite” de l’hydrogène neutre, le gaz dans lequel baignent galaxies, Soleil et planètes. Par les transformations qui, elles, sont permises, elle apparaît reliée aux raies non-interdites du système planétaire et, peut-être à des harmoniques, dont celui de 0,021 cm/s2 donné par l’accélération centrale à 5,32 UA. On peut en déduire que la cosmogonie du système solaire paraît étroitement conjointe à l’hydrogène, puisqu’en suivant nos deux modèles astrologiques, les cycles dans leur ordre chronologique et les fonctions planétaires dans l’ordre R.E.T., deux modèles de l’hydrogène, celui des transitions énergétiques (atome excité ou ionisé) et celui de l’atome neutre se sont imposés, de façon différente, pour que le produit x, y, donne exactement la constante Mars arrondie à 1/6, les valeurs d3, d′3 du tableau XXVIII sont moyennées et corrigées :
TABLEAU XXX — Coordonnées x, y du segment de branche d’hyperbole équilatère demi-axes a et b = 0,166.
| Planète |
x |
Planète |
y |
| Soleil |
0,081 |
Pluton |
0,342 |
| Vénus |
0,117 |
Neptune |
0,237 |
| Mercure |
0,123 |
Uranus |
0,225 |
| Jupiter |
0,144 |
Saturne |
0,193 |
| Mars |
0,166 |
Mars |
0,166 |
| |
| Lune |
0,039 |
Lune |
0,712 |
| Terre |
0,123 |
Terre |
0,225 |
| Cérès |
0,280 |
Cérès |
0,100 |
Lune, Terre, Cérès, n’ayant pas de partenaire connu, les valeurs y sont déterminées par les seules données d3 qui leur correspondent au tableau XXVIII.
Pour simplifier l’équation d’une courbe ou pour en étudier certaines propriétés, on peut avoir intérêt à changer les axes de coordonnées, les déplacer ou effectuer une rotation sans déplacement. L’équation de l’hyperbole équilatère rapportée à ses asymptotes est y = k / x ou k = y ⋅ x. La formule appliquée aux données x, y, du tableau XXX donne k = Mars2 (0,1662). Une rotation de 45° rapporte l’hyperbole à ses axes de symétrie et transforme les coordonnées x, y, en coordonnées X, Y. La formule k = y ⋅ x devient :

Qui ne change pas la valeur de k adoptée 0,1662, et par conséquent, 2 ⋅ k = 0,0555… ou 1/18.
TABLEAU XXXI — Transformation des cordonnées x, y, de l’hyperbole planétaire en coordonnées X, Y, après rotation de 45°. (Résultats arrondis à la 3e décimale).
Couple
(p, p′) |
x
(p) |
y
(p′) |
X
(p, p′) |
Y
(p, p′) |
| Soleil - Pluton |
0,081 |
0,342 |
0,300 |
± 0,185 |
| Vénus - Neptune |
0,117 |
0,237 |
0,251 |
± 0,085 |
| Mercure - Uranus |
0,123 |
0,225 |
0,247 |
± 0,073 |
| Jupiter - Saturne |
0,144 |
0,193 |
0,238 |
± 0,035 |
| Planète |
x |
y |
X |
Y |
| Mars |
0,166 |
0,166 |
0,236 |
0 |
| Lune |
0,039 |
0,712 |
0,531 |
0,476 |
| Terre |
0,123 |
0,225 |
0,247 |
0,073 |
| Cérès |
0,280 |
0,100 |
0,268 |
0,127 |
Le but de la transformation est de déceler la nouveauté : une relation inaperçue entre les lignes, entre les angles. Ce qui suit concerne les angles. Une hyperbole, comme tous les membres de sa famille de coniques (ellipse, parabole) a deux foyers : F et F′. De l’origine 0 des coordonnées à la distance F, la distance focale C, sur l’axe des abscisses (X) est égale à 2 ⋅ √k, qui donne C = 1 /3 pour k = 1/62. L’angle formé par le rayon vecteur F-planète et l’axe des X se calcule par : tan P̂ = Y / (C − X). D’où le tableau XXXII :
TABLEAU XXXII — Détail du calcul de tan P̂ à partir des données du tableau XXXI.
| Couple |
C − X |
Y / (C − X)
= tan P̂ |
P̂ |
| Soleil - Pluton |
0,034 |
± 5,44 |
± 79°,6 |
| Vénus - Neptune |
0,083 |
± 1,04 |
± 45°,8 |
| Mercure - Uranus |
0,087 |
± 0,84 |
± 40° |
| Jupiter - Saturne |
0,094 |
± 0,37 |
± 20°,3 |
| Mars |
0,098 |
0 |
0° |
| |
| Lune |
−0,198 |
−2,41 |
112°,6 |
| Terre |
0,087 |
0,847 |
40°,3 |
| Cérés |
0,065 |
1,96 |
63° |
Valeurs arrondies à la 3e décimale. Dans la marge d’incertitude du tiers de degré, à partir du foyer F, le classement des planètes en R.E.T. est restitué par trois zones angulaires sensiblement égales :
| Zone |
Planètes |
Positions |
Étendue |
| R |
Soleil
Vénus
Mercure |
79°,6
à
40° |
39°,6 |
| E |
Jupiter
Mars
Saturne |
20°,3
à
−20°,3 |
40°,6 |
| T |
Uranus
Neptune
Pluton |
−40°
à
−79°,6 |
39°,6 |
La logique des significations planétaires a permis de concevoir une organisation ternaire. Il était difficile de choisir la figure géométrique qui en témoignerait mieux qu’une autre. Plus difficile encore d’imaginer que les données astrométriques aboutiraient à délimiter deux zones intercalaires d’une valeur angulaire égale à celle de chaque famille du R.E.T. Soit, en valeur absolue : (Mercure-Jupiter) + (Uranus-Saturne) = 39°,4.
La bissectrice de ±79°,6 correspond aux angles ±39°,8 du couple Mercure-Uranus. À nouveau, la bissectrice de cet angle, soit ±19°,9 est proche de l’angle ±20°,3 du couple Jupiter-Saturne. Si les limites des trois groupes paraissent relever d’une division géométrique binaire, l’angle ±45°,8 de Vénus-Neptune reste à justifier. Peut-être par la Lune qui se place à la bissectrice de l’angle 180° − 45°,8 ; soit 45°,8 + (134°,2/2) = 112°,9. Cérès, le plus important des astéroïdes, du côté des planètes au-delà de Mars dans le R.E.T. lui est opposée, à 4° près (113° + 63° = 176° au lieu de 180°). Mais la relation vaut aussi pour Vesta et, sans doute, pour quelques autres astéroïdes.
Il ne s’agit pas de positions concrètement observables, mais d’une représentation de relations réelles, non visibles entre les planètes principales du système solaire, La figure 16 en donne l’illustration géométrique. La figure 17 en donne une autre en associant à l’hyperbole sa courbe inverse : la lemniscate. Les deux images, la lemniscate (du grec lêmniskos : ruban) et l’hyperbole caractérisent visuellement l’originalité des deux groupes et la symétrie qui les réunit.
Note : la tangente de l’angle au foyer F se calcule directement à partir de x par la formule :

(Coefficients déterminés par la valeur 1/6 des axes a et b).
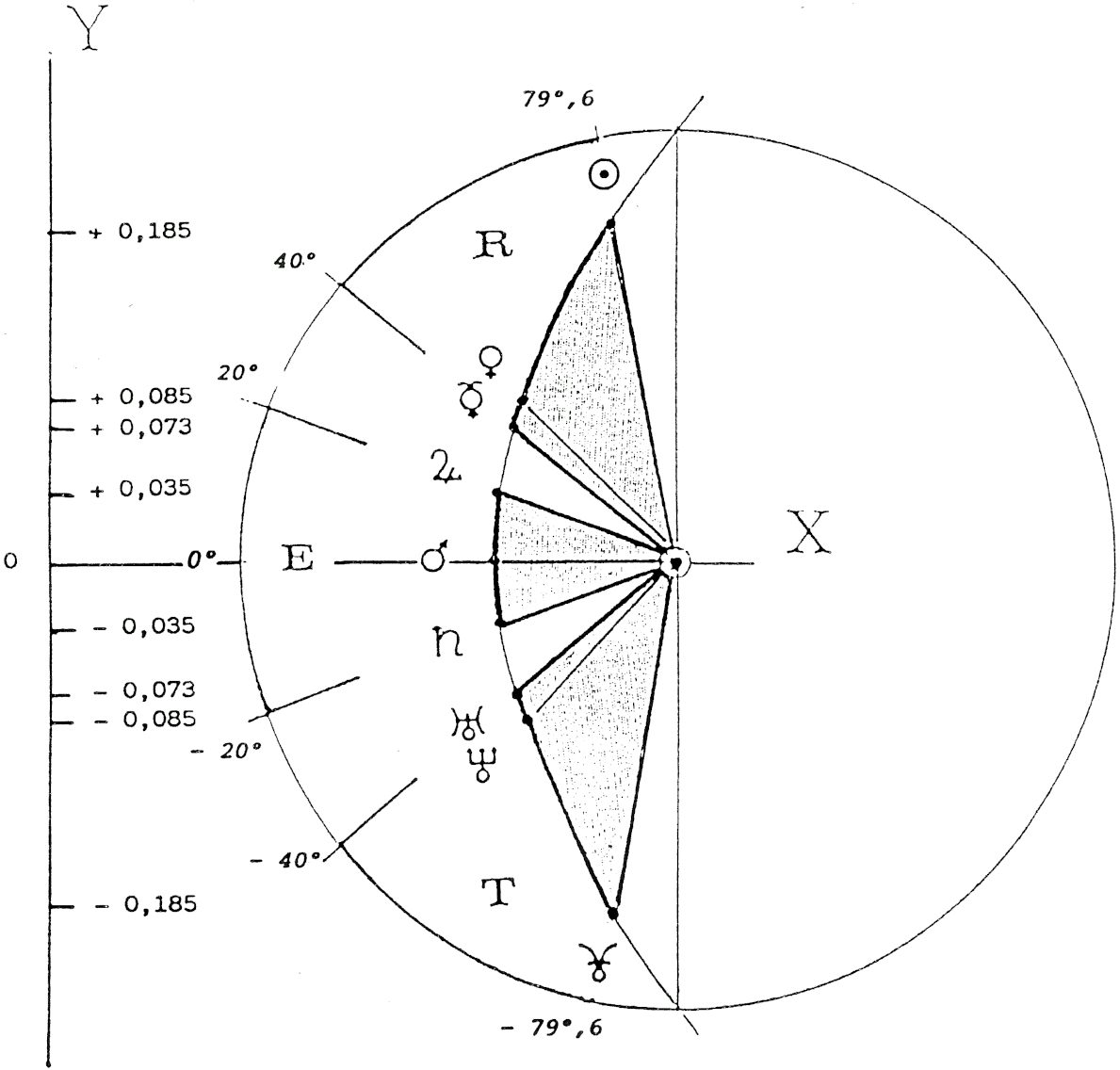
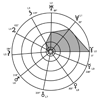
FIG. 16 — Tripartition du R.E.T. en trois secteurs sensiblement égaux de 40° après transformation des coordonnées x, y, en X, Y par rotation d’axe de 45° (tableau XXXII). La Lune et Cérès, non représentés, se situent à 113° et −62° de Mars 0°.
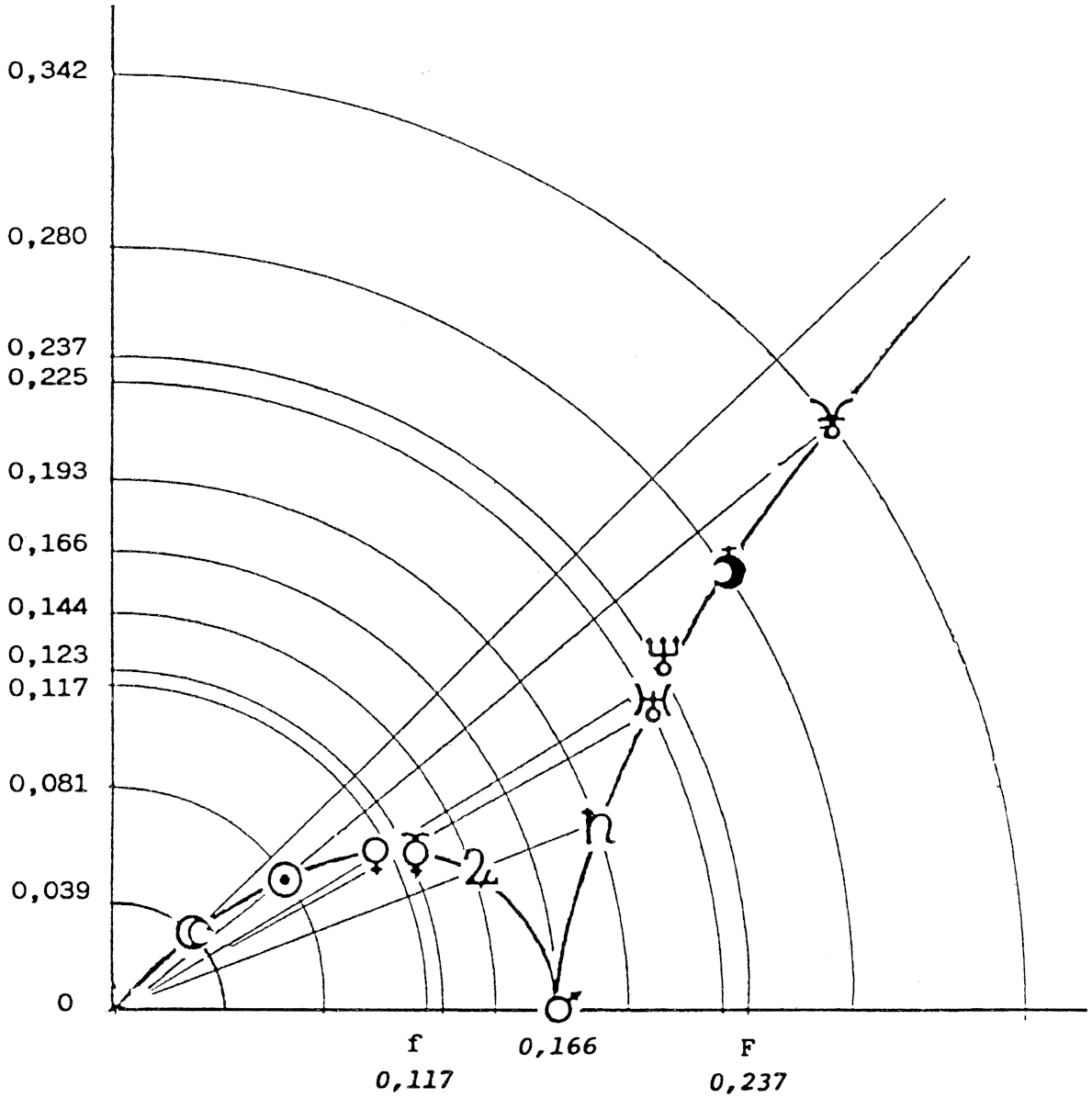
FIG. 17 — La lemniscate, courbe fermée, l’hyperbole, courbe ouverte, sont des courbes inverses, liées par la formule x ⋅ y = constante (k). Sur cette figure la constante = 0,1662 (d3 de Mars). Les orbites inférieures à 0,166 se situent sur la courbe d’un quart de lemniscate (0 à 0,166), les supérieures à 0,166 se situent sur un segment d’hyperbole. Ce qui satisfait la relation d3 × d′3 = 0,1662, et permet une bonne représentation de la symétrie inverse des couples planétaires du R.E.T.
Article suivant — 2.5/1. Cosmogonies comparées
[1] Astronomie. Collectif dirigé par Philippe de La Cotardière. Chapitre sur le Soleil par Roger-Maurice Bonnet, Monique Pick, Elisabeth Ribes. Éd. Larousse, 1989.