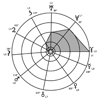
Demi-grands axes et gravités
La cosmologie concerne aussi bien le sacré que le profane, mais l’on peut faire une distinction de principe entre cosmogonie et cosmologie. La cosmogonie raisonne sur l’état véritable du monde, tandis que la cosmologie “est proprement une physique générale et raisonnée qui, sans entrer dans les détails trop circonstanciés des faits, examine du côté métaphysique les résultats de ces faits mêmes, fait voir l’analogie et l’union qu’ils sont entre eux, et tâche par là de découvrir une partie des lois générales par lesquelles l’univers est gouverné.” Tous les scientifiques ne souscriront pas à cette définition de Bescherelle (aîné) qui place sur le même plan les explicatives rationnelles fondées, depuis la domination des sciences exactes, sur les constantes physiques, et des systèmes philosophiques étrangers à ces sciences comme à leurs paradigmes. En France, voire en Occident, il est d’usage de qualifier de tels systèmes “d’irrationnels”… en hommage possible à Descartes qui, dans son système, fondait la certitude de la géométrie sur la connaissance de Dieu.
Cosmogonies ou cosmologies rivalisent en surnombre comme autant de dieux grecs en lice pour renverser Jupiter et gouverner l’Olympe, c’est-à-dire, en termes modernes : l’horizon des réalités et des connaissances contemporaines [1]. Le philosophe-physicien Pierre Duhem a consacré neuf volumes et un demi-siècle de sa vie à l’Histoire des doctrines cosmologiques de Platon à Copernic. Pour Pierre Duhem, il n’y a pas eu de commencement de la recherche scientifique : “toujours on peut remonter à d’autres éléments qui ont permis ce qui suivit.” [2] Dans son œuvre, les penseurs se suivent, complexifiant les hypothèses d’une génération l’autre sous la contrainte des faits mesurés… donc, des nombres… puis les simplifient pour les ériger en une nouvelle synthèse, aussi provisoire que les précédentes.
La pluralité des cosmogonies du système solaire et des cosmologies métaphysiques qui font plutôt désordre quant au passé, est avantageusement compensée, de nos jours, par les exploits cosmologiques exceptionnels du Big Bang. Les savants du macro comme du microcosme ne tarissent pas d’éloges sur ses vertus unificatrices. Grâce à cette cosmologie imparable, nous savons incidemment qu’un être, l’Homo sapiens, de moins de 2 mètres de haut, 60 cm de tour de tête pour un poids encéphalique d’1 kg et demi, avec une durée de vie inférieure à la centaine, a réussi à calculer (ou se persuader) que son univers est né il y a 15 milliards d’années, et qu’il était petit, très petit, infiniment petit jusqu’à une certaine limite, et très chaud, très, très chaud, infiniment très chaud… et très dense, très, très dense, infiniment dense (sans exagérer), si bien que Dieu, infiniment bon, infiniment parfait, infiniment aimable, ne pourrait guère se reconnaître dans cet œuf infiniment petit, dense, chaud et vieillot, conforme aux Constantes Physiques, conçu… à partir, savez-vous de quoi ? Des mesures de la vitesse de la lumière, prises sur une pseudosphère (la Terre) de 13000 km de diamètre, par des cerveaux de moins d’1 kg et demi qui n’ ont pas reculé devant des extrapolations des milliards de milliards de fois supérieures à leurs mesures et leurs dimensions d’observateurs terrestres. Comment ne pas être fier de tant d’audace… incontrôlable, malgré l’affirmation toujours répétée que “pour être scientifique, un phénomène doit être reproductible et attesté par des témoins différents” !?
Cette vitesse de la lumière que personne, expérimentalement, n’a jamais mesurée sur place au-delà de la Lune, ce gigantisme, ces prodiges de l’esprit contenu dans 3 livres de matière grise, n’ont fait qu’engendrer des orgueils bouffis d’intolérance envers leurs précurseurs astrologisants. Et songer à une synthèse de recherches millénaires en se pliant aux anathèmes de son époque ne peut aboutir qu’à une œuvre boiteuse. Partielle parce que partiale. il y a de fortes chances, par conséquent, pour que les triomphantes aventures de Big Bang-Boum ne se révèlent sujettes à des révisions périodiques.
Pour éviter la liste toujours ouverte des hypothèses cosmogoniques rejetées ou éjectables on peut évoquer quelques uns des arguments, des données et des scénarios le plus souvent utilisés.
La première règIe, proche de la certitude absolue, veut que sitôt une hypothèse formulée, la suivante n’est pas loin pour la liquider à partir de son inadéquation avec des données nouvelles ou anciennes inexpliquées.
Une théorie satisfaisante sur l’origine du système solaire doit répondre des caractéristiques principales de sa structure. À savoir :
- Coïncidence, à l’exception de celle de Pluton, du plan des orbites planétaires avec le plan de l’équateur solaire.
- À l’exception de Mercure et Pluton, faibles excentricités des orbites.
- Translation des planètes dans le même sens que celui de la rotation du Soleil sur son axe.
- La direction de la rotation axiale des planètes, à l’exception de Vénus et d’Uranus, coïncide avec celle de leur révolution autour du Soleil.
- Distribution présumée cohérente des distances moyennes au Soleil (demi-grands axes).
- Masse des planètes, globalement de 750 fois inférieure à celle du Soleil, alors qu’il leur revient 98 % du moment cinétique de l’ensemble du système solaire.
- Classement des planètes en deux groupes (telluriques et géantes) suivant leurs propriétés physiques et, certaines, astrométriques (distances, nombre de satellites, rotation).
On pourrait continuer avec les astéroïdes et les planètes couplées (Terre-Lune, Pluton-Charon). Il y a déjà matière à conjectures et remises en question successives pour peu qu’une explication empêche ou chasse celles d’autres caractéristiques. Les hypothèses performantes se doivent de justifier un maximum de caractéristiques, mais les priorités sont changeantes. Un astrophysicien appréciera une hypothèse convenable sur les causes originelles de la partition des planètes principales en deux groupes aux propriétés physiques distinctes. Une loi des distances, séduisante pour un mathématicien, lui paraîtra secondaire si elle ne se rattache pas à une physique connue, orthodoxe ou révolutionnaire, car l’Univers est une arène de premier choix pour les théories rivales.
Les scénarios imaginables, après avoir opposé les catastrophistes aux évolutifs, se sont multipliés par les dosages différents de catastrophes (marées, perturbations créees par des masses étrangères au système solaire) et de phénomènes évolutifs (planètes formées par un développement sans accidents).
Les éléments constituants privilégiés d’une cosmogonie dépendent du niveau des connaissances d’une époque, mais on ne peut pas passer entièrement sous silence les prédilections politiques, religieuses, philosophiques. Ce qui a fait dire à Pierre Duhem : “Les hypothèses cosmogoniques sont aussi anciennes que l’humanité et leur histoire reflète celle des civilisations.”
À un plus grand nombre d’éléments, par rapport aux cosmogonies anciennes, les modernes ont ajouté des processus ou des forces jusqu’alors inconnus et qui se soutiennent, se conjuguent, se relaient ou s’engrènent dans un scénario de création du monde où chaque auteur doit mobiliser autant d’imagination que de savoir et d’astuces. Après les tourbillons de Descartes, il faut davantage user de la pression de la lumière, du vent solaire, de l’électromagnétisme, l’agitation thermique, la contraction gravitationnelle, les chocs et demi-chocs des particules, molécules, grains et poussières cosmiques. Le cosmologue inspiré brasse ces données rebelles dans un insondable pétrin.
Un anthropologue pourrait se divertir à dénombrer les modèles en vogue suivant les époques, les pays et, pourquoi pas, les planètes et Signes dominants des faiseurs d’univers. Comme pour une courbe en cloche de Gauss, ou pour une course, les favoris ont la cote et l’on ne se fie guère aux outsiders. Les planètes jumelles chères à A. Dauvillier [3] ne sont pas aussi prisées que les anneaux ou les essaims générateurs d’astres non accouplés. Les éléments de notre cosmogonie astrologique dépassent le modèle de couples planétaires indépendants et introduisent celui d’un ensemble formé de duos solidaires.
S’il y a des erreurs pardonnables dans les scénarios proposés, il est des questions auxquelles une cosmogonie crédible doit répondre (ne serait-ce que pour en parler) sous peine d’être irrévocablement recalée. Le moment angulaire du système solaire fait partie des épreuves fatales aux plus belles constructions. Un physicien, Ali Mehmet Celâl Sengör, s’en préoccupe encore : “Bien que le Soleil représente près de 99 % de la masse du système solaire, 98 % du moment angulaire du système réside (en effet) dans les planètes.” [4]
Comme d’une vulgaire civilisation sumérienne ou d’une réunion d’astrologues au Vel’ d’Hiv, Evry Schatzman se débarrasse des réalités gênantes. En reprenant l’hypothèse de Laplace d’une nébuleuse qui, d’un rayon égal à la distance actuelle de Pluton, va en se contractant tourner de plus en plus vite, et engendrer successivement des anneaux, puis des planètes… il reconnaît que de contraction en contraction, le nuage primitif devrait former finalement un Soleil en rotation rapide, à la vitesse de 472 km/s à l’équateur. En fait, le Soleil à une vitesse de rotation de 1,9 km à l’équateur, 250 fois plus faible que la vitesse attendue. Pour faire face à ce fiasco encore plus retentissant que la “loi” de Titius-Bode, E. Schatzman ne fait pas appel à Sainte Rita mais au bon vieux naturel : “… Il y a donc eu un mécanisme de freinage qui a ralenti ces étoiles, et cela pendant les dernières étapes de leur formation… II est donc inutile de chercher à tirer de notre imagination les causes du ralentissement du Soleil au cours de sa formation. Ces causes seront trouvées dans l’étude de la Nature… La vieille objection (le moment angulaire) à l’hypothèse de Laplace (la nébuleuse en contraction) tombe d’elle-même du moment que la formation, des étoiles jaunes (le Soleil est de la famille) avec un lent mouvement de rotation est une loi naturelle.” [5]
“Voilà pourquoi votre fille est muette…” dirait Molière. Sans appel au naturel, recours singulier chez un rationaliste, le moment angulaire du Soleil (produit : masse, vitesse, rayon) est récupérable, non seulement par les couples planétaires (tableau XIV) du système solaire, mais par les distances dg (tableau XXV), les vitesses V linéaires et les masses actuelles.
La vitesse linéaire moyenne étant proportionnelle à 1 / √L (L, demi-grand axe), on obtient en unités terrestres le produit d̄g × V̄ par la formule : (0,0847 × L̄−1/6) / ḡ1/3, expression dans laquelle 0,0847 = d̄g de la Terre.
TABLEAU XXXIII — Calcul du produit distance, vitesse, masse pour chaque planète avec les distances d̄g obtenues par le rapport L̄ / ḡ (détail tableau XXV).
| Planète |
Rayon
d̄g
(UA) |
Vitesse
V̄
(l = 1) |
Masse
m̄
(l = 1) |
Produit
d̄g ⋅ V̄ ⋅ m̄
|
| Vénus |
0,079 |
1,176 |
0,815 |
0,076 |
| Mercure |
0,086 |
1,607 |
0,055 |
0,008 |
| Terre |
0,085 |
1 |
1 |
0,085 |
| Jupiter |
0,105 |
0,438 |
318 |
14,6 |
| Mars |
0,134 |
0,811 |
0,107 |
0,012 |
| Saturne |
0,170 |
0,324 |
95 |
5,23 |
| Uranus |
0,232 |
0,228 |
14,6 |
0,77 |
| Neptune |
0,251 |
0,182 |
17,2 |
0,79 |
| Pluton |
0,705 |
0,159 |
0,002 |
0,0003 |
| Soleil |
105 × 0,2 = 21 |
Somme = 21,6 |
Résultats plus proches du Soleil que ceux du tableau XIV mais sans former de couples et sans appel à Cérès… d’une masse trop faible d’ailleurs pour modifier la somme déterminée surtout par les deux géantes, Jupiter et Saturne. Au lieu d’un seul moment angulaire, en voilà deux, également hérétiques. Si l’on en rejette aucun, le défi cosmogonique se résume à expliquer ou imaginer le passage des dg individualistes aux demi-grands axes couples et moyennes. Les gravités planétaires (produit densité rayon) rarement prises en compte dans les cosmogonies convenues sont au centre du problème. Elles devraient en donner la solution. Cette démarche astrologique restitue les moments perdus sans réhabiliter la nébuleuse contractile de Laplace. En considérant, par hypothèse, les distances dg comme des distances originelles, le système solaire se serait dilaté et non pas contracté. De plus, il faudrait expliquer par quels processus, naturels ou accidentels, l’ordre des distances dg (Vénus, Mercure-Terre, Jupiter, Mars) se transforme en ordre L (Mercure, Vénus, Terre, Mars, Jupiter)… les planètes lentes, de Saturne à Pluton, conservant le même ordre. La densité et le rayon seront encore les facteurs discriminatoires décisifs.
Les hypothèses modernes ne s’élèvent pas contre la nébuleuse en chute pour prôner un noyau en expansion, mais reviennent, dans la foulée d’une mode de l’ordre jaillissant du chaos, à des collisions cataclysmiques… qui auraient séparé les protoplanètes en deux ou trois astres différents en bouleversant les trajectoires initiales.
Selon une enquête serrée de Willy Benz, “des simulations numériques montrent que la formation de Mercure résulterait d’un impact géant avec une autre protoplanète” [6]. Après les réserves d’usage, aussi utiles que les onctions de la politesse, il se prononce : “Le scénario d’impactant a néanmoins des caractéristiques très intéressantes. Il permet d’expliquer la densité très élevée et anormale de Mercure dans le contexte général de la formation des planètes.” Et, puis, en généralisant : “Le même mécanisme physique, celui des collisions, qui est responsable de la croissance des planètes, est également à la base de leurs caractéristiques physiques particulières. De plus, il existe ailleurs dans le système solaire d’autres évidences indirectes d’impacts géants. Comme nous l’avons vu, la Lune de la Terre s’est ainsi très probablement formée dans une collision similaire entre une proto-Terre et un projectile de la taille de Mars. L’axe de rotation anormalement incliné d’Uranus pourrait, de même, être le résultat d’une collision géante.”
Ce qui l’amène logiquement à constater : “Les théories catastrophiques ont toujours eu beaucoup de mal à être acceptées et on leur a souvent préféré les théories d’évolution. Néanmoins, au vu du nombre grandissant de preuves indirectes d’impacts géants lors des premiers jours de notre système solaire, il ne semble plus y avoir aujourd’hui d’autre issue possible” (c’est moi qui souligne).
Par la taille, la masse et la densité, Vénus ressemble aussi à la Terre. Les coordonnées X, Y (Tableau XXXI) de Mercure-Terre, sont identiques, et celles de Mercure, Vénus, très voisines, comme celles de leurs symétriques, Uranus, Neptune. Il est tentant d’oublier les constitutions physiques différentes pour réunir toutes les masses et imaginer un satellite unique du Soleil ou une étoile binaire. Les données actuelles conduisent à une Masse d’environ 447 fois celle de la Terre et à un rayon (moyenne cubique des rayons moyens) de 13,3 fois celui de la Terre. Il en résulte une gravité moyenne de 2,53… proche de celle de Jupiter, et une densité moyenne théorique de 1,05… de l’ordre des densités des planètes gazeuses. En appliquant la formule, 9 j × √(L̄ / ḡ), avec L̄ = 0,135 UA, dg de Mars centre du système, un corps de cette masse et gravité, donne une période Tg de 2,09 j et une nouvelle distance dg de 0,032 UA. On en déduit une vitesse orbitale linéaire de 166,5 km/s, une moyenne kilométrique rencontrée précédemment (tableau XXVII) à l’occasion des vitesses mises en couples.
Tout autant que le moment angulaire, l’amateur de cosmogonies ne doit rien ignorer de la “limite de Roche”. Cet astronome, mathématicien et géophysicien français (1820-1883) a calculé la distance en deçà de laquelle un satellite est détruit par les forces de marée dues à l’attraction du corps autour duquel il gravite. Dans le cas d’un objet sphérique rigide en orbite autour du Soleil, cette limite est :

Pour avoir cette distance critique Dlim on multiplie donc le rayon du corps principal R3 par la racine cubique du rapport des densités (celle du corps principal ρ3 au numérateur) et par le coefficient 2,45. Application illustratrice : en adoptant dans l’ensemble dg du tableau XXV, la distance 0,049 UA comme première distance, et pour densités, 1,41 (Soleil !) et 1,05 (protoplanète), la formule ci-dessus conduit à : 2,70 × 0,0049 = 0,1324 soit une distance Dlim proche de la distance dg de Mars. La distance 0,049 obtenue par la gravité solaire et la moyenne des couples planétaires, aurait-elle fait craquer un corps hypothétique à 0,132 UA (toutes ces distances étant relatives) ? Le passé pourrait nous le dire. Au présent, dans la recherche des processus de formation du système solaire, la limite de Roche est utile tantôt pour faire craquer un astre, tantôt pour éviter qu’il ne craque en un mauvais lieu. C’est une limite d’achoppement aussi impitoyable que la vitesse du vent (solaire), la température, la pression de la lumière, l’âge du système planétaire sinon de son Capitaine.
La clarté demande de réduire au plus simple. Ce qui ressort des données L et L / g traitées dans cette cosmogonie ne permet pas encore de trancher radicalement entre une étoile binaire, une unique en duplication, des anneaux ou une protoplanète brisée. Le certain est la démonstration de directions relatives privilégiées : angles du système L liés aux rapports des demi-grands axes, et angles du système d3 liés à la rotation équatoriale solaire par la constante de 25 jours, moyenne géométrique des couples. Ces deux systèmes, quoique différents, sont également ordonnés et constitués de deux parties symétriques. Jupiter domine les couples de demi-grands axes L, Mars les couples de distances dg ou d3. En l’absence provisoire de données sur des systèmes planétaires comparables au nôtre, il est peut être trop tôt pour se prononcer définitivement sur un scénario de transformation de d3 ou dg en L. Enfin, il peut être vain d’en chercher la genèse puisque ces données et leurs relations sont contemporaines. Il est plus important, astrologiquement, d’en chercher les voies d’efficacité.
L’astronome s’évertue à imaginer comment, en quelles circonstances spatiales et temporelles, le fluide est devenu solide, les densités ont changé, les particules se sont groupées, les masses accrues ou diminuées. Il lui faut des collisions, des températures, des limites et des principes d’organisation du passé. L’astrologue, dans ces Éléments de cosmogonie, n’a rien à réorganiser, les nombres s’organisent d’eux-mêmes sans regard en arrière. Un lycéen nanti d’une calculette n’aura rien à imaginer en contrôlant la cohérence des formules et la marge de précision des résultats. Un peu plus curieux, au plan des explications causales, il pourrait revenir aux cosmogonies tenant compte des champs magnétique et électrique solaires, les seules confirmées dans leur principe par les relations entre les demi-grands axes et les termes spectraux de l’hydrogène.
Christian Birkeland (1867–1917) a été le premier à prendre en considération le champ magnétique solaire. Selon sa théorie, le Soleil aurait émis des ions que le champ magnétique aurait disposés en orbites circulaires et concentriques autour du Soleil. L’Encyclopédie Atlas d’astronomie [7] cite également H. P. Berlage qui “tint compte de l’effet du champ électrique solaire sur des ions émis par le Soleil lorsque ce dernier était entouré d’une vaste enveloppe aplatie par la rotation. […] Il trouva que, dans ces conditions, des ions positifs de masses atomiques différentes auraient atteint des positions d’équilibre à des distances différentes du Soleil ; ces ions auraient servi de noyau de condensation et auraient été ainsi à l’origine de la formation des anneaux de matière.” Un auteur contemporain, Hannes Alfven (1908), suppose que le Soleil, au cours de son mouvement dans l’espace, aurait traversé un nuage gazeux ; les atomes de ce dernier, capturés par le Soleil, auraient acquis une énergie cinétique suffisante pour s’ioniser. Les forces magnétiques auraient alors dominé les forces gravitationnelles et les ions se seraient mis en orbite autour du Soleil. Mgr Georges Henri Lemaître (1894–1966), astrophysicien et mathématicien belge, a été le premier à envisager un univers en expansion issu de l’explosion d’un atome primitif. Le système solaire n’a pas été épargné par sa cosmogonie radioactive où le Soleil, considéré comme un atome, éjecte des planètes-atomes éjectant à leur tour des satellites radioactifs.
Les hypothèses inspirées par l’atomistique sont, de loin, plus rares que les mécaniques. En théorie, elles ont été tout autant réfutées. Sans avoir d’atome explosif à proposer, les rapports des demi-grands axes, justifiés par le formalisme de l’atomistique tranchent en leur faveur d’une façon décisive. Dans un domaine flou, c’est une certitude considérable. Elle ne l’est pas assez pour choisir entre une étoile unique ou une binaire… ce qui n’étonnera pas les astrologues conditionalistes qui disposent d’un modèle conceptif (un Logoscope) où le binaire peut se transformer en unique et l’unique en multiple. Un modèle qui se prête, comme dirait Hubert Reeves, à divers scénarios “astucieux” recevables… s’ils ne sont pas conçus par des astrologues. L’unique serait une pulsante engendrant ses anneaux et ses planètes dans le plan équatorial au sein de son halo sphérique aux fluctuations périodiques (et pendulaires !). Scénario peu différent de celui proposé dans Nombres et Formes du Cosmos [8]. En détachant une masse partielle de la principale, en binaire par unique dédoublé, le couple crée ses planètes par interactions gravifiques et interférences “ionisantes”. Cette hypothèse est la plus conforme aux représentations géométriques induites par les données traitées (coniques à deux foyers). Elle justifie les couples en symétries et l’existence d’un plan médian séparateur. Les masses de Jupiter et Saturne, ainsi qu’on l’admet communément seraient les premiers et principaux vestiges d’un méga-astre initial compagnon-satellite du Soleil. selon les distances actuelles, le plan médian passe dans la zone des astéroïdes.
Comme les ésotéristes de tous temps, quelques astrophysiciens de ce siècle et du siècle dernier, n’ont pas hésité à réunir, dans leurs essais d’explicatives scientifiques de la genèse du monde, l’atome à l’étoile, l’infiniment petit à l’infiniment grand. Ils rejoignent ou imitent en cela les démiurges des cosmologies sauvages. Par rapport aux essais antérieurs, mythologiques ou rationnels, celui-ci apporte la démonstration numérique d’une identité formelle entre “macrocosme et microcosme”. Les astrologues qui ont fait leur credo du petit qui chausse dans le grand par homothétie analogique, se sont prononcés sur cette correspondance chiffrée par un profond silence… en attente soucieuse d’une transplutonienne de moins en moins probable, comme j’ai pu l’annoncer il y a une vingtaine d’années.
Outre la réunion du grand et du petit, du haut et du bas selon la règle d’Hermès Trismégiste, la cosmologie antique s’est aussi employée à réunir Temps et Structure, ou un déroulement chronologique et un ordre d’un absolu intemporel. D’après Jean-Pierre Vernant [9] commentant les Travaux et les Jours du poète Hésiode (VIIIe–VIIe siècle av. J.-C.), “Le mythe des âges nous offrirait alors l’exemple le plus ancien d’une conciliation entre le point de vue de la genèse et celui de la structure, d’une tentative de faire correspondre terme à terme les stades d’une série temporelle et les éléments d’une structure permanente.”
Pour les astrologues conditionalistes, les stades temporels sont en rapport avec les cycles héliocentriques du système L (demi-grands axes),les éléments de la structure permanente, avec le système L / g qui restitue l’ordre de classement des planètes dans le modèle R.E.T. Les couples planétaires ne sont pas les mêmes et les périodes, à l’exception de Pluton (220 j) sont inférieures au cycle de Mercure (88 j) dans le système dg, supérieures à ce cycle dans le système L. On peut être tenté d’attribuer les premières à la chronologie de la gestation… hypothèse aussi aisément vérifiable, pour un généticien, que celle de la théorie des âges, comme on peut se demander comment ces couples planétaires coexistent en efficacité. Faut-il évoquer le manifeste (cycles héliocentriques T) et le virtuel (cycles Tg) ? Ou voir dans la chronologie un ordre de développement plus déterminant que la structure qui en contient néanmoins le programme ? En termes mythologiques, la chronologie correspond évidemment à la chute d’Adam et Ève, chassés du paradis de l’intemporalité. Mais, à l’inverse du mythe, la chronologie (système L) apparaît avec la suppression de g qui désigne l’accélération d’une chute !
En attendant de réunir par un discours explicite les systèmes L et L / g, l’équation ci-après réduit à la plus simple synthèse possible la chronologie, représentée par V2 (vitesse2 sur orbite), et la structure (ou ordre R.E.T., représentée par : 2 × (V32 − 452), puisque cette expression, avec V32 (vitesse2 circulaire à la distance d3) restitue Vg2 (carré de la vitesse circulaire à la distance dg).
 ou
ou
 avec :
avec :

En raison des proportionnalités de g avec le rayon par la densité ou avec G ⋅ m / r2, de la force centrale f3 avec V2 / L ou G ⋅ M3 / L2, des vitesses avec 1 / √L… ces deux expressions sont transformables en de plus savantes et de moins lisibles. Sous cette forme :
- g = intensité moyenne de la gravite à la surface de l’astre.
- f3 = intensité de la force centrale à la distance moyenne du même astre.
- V = sa vitesse linéaire moyenne pour sa période T de révolution sidérale.
- V3 = vitesse linéaire à la distance d3.
En dehors du coefficient 8, on peut adopter n’importe quel système d’unités, en veillant à respecter son homogénéité.
Pour extraire une ou plusieurs cosmogonies de l’équation ci-dessus, il faut connaître les relations entre les vitesses. Ainsi, l’expression : 2 × 452 = 63,642 en km2/s2, correspond à la vitesse parabolique d’un astre gravitant à la distance de 0,438 UA du Soleil. La vitesse linéaire orbitale de la Terre est de 29,785 km/s. Par rapport au Soleil, la vitesse qui permettrait à notre astre de changer d’orbite sans quitter le système solaire sera donc égale à la racine de 2 fois 29,7852 soit 42,12 km/s. À cette vitesse, l’astre quitte son mouvement circulaire s’il se trouve sur l’orbite de distance D = 1 UA. Pour échapper à l’attraction terrestre lorsqu’on se trouve à sa surface, altitude zéro (distance égale au rayon moyen), il faut une vitesse cosmique égale ou supérieure à la racine de 2 fois g, gravité à la surface, que multiplie le rayon terrestre moyen. Soit : √(2 ⋅ g ⋅ r), ou √(2 ⋅ G ⋅ m / r) = vitesse parabolique par rapport à la surface de la Terre, et non par rapport au Soleil. Pour g = 9,80 m/s2 et r = 6 378 000 m, il faudra, pour décoller de l’attraction terrestre et s’éloigner dans l’espace cosmique, posséder un engin capable d’atteindre 11,18 km/s, deuxième vitesse cosmique ou vitesse de libération par rapport à la Terre.
La vitesse supplémentaire nécessaire pour qu’un appareil cosmique lancé de la Terre quitte le système solaire dépend de la direction dans laquelle il sortira de la sphère d’action terrestre par rapport à la direction du mouvement orbital de la Terre.
Entre deux corps de masses m et m′, le rayon, Rc, de la sphère d’action du corps m, s’obtient par : Rc = L ⋅ (m / m′)2/5. Avec L = 1 UA pour le rapport des masses Terre/Soleil, le rayon de la sphère d’action terrestre égale, sensiblement, 930 000 km.
Si l’on prend pour vitesse héliocentrique de la Terre sa vitesse circulaire V de 29,785 km/s, la vitesse supplémentaire dans le sens du mouvement orbital, doit être égale à la différence entre la vitesse parabolique et la vitesse circulaire. Soit : 42,12 − 29,785 = 12,34 km/s.
Dans le sens opposé à la translation orbitale, ces deux vitesses s’additionnent : 42,12 + 29,785 = 71,9 km/s.
La 3e vitesse cosmique minimale par rapport à la Terre, V3, s’obtient par : V3 = √(11,182 + 12,342) = 16,65 km/s. Expression banale d’un calcul d’hypoténuse pour un triangle rectangle dont un côté serait la vitesse parabolique (11,18 km/s) par rapport à la surface, et l’autre côté, la vitesse supplémentaire (12,34 km/s) dans le sens du mouvement orbital. La 3e vitesse cosmique maximale par rapport à la Terre, conserve la vitesse parabolique par rapport à sa surface, mais avec la vitesse supplémentaire maximale, de façon que : V3 = √(11,182 + 71,92) = 72,76 km/s.
Pour s’évader du système solaire à partir de la surface terrestre, il faut donc, selon la direction choisie, une vitesse départ (à la distance r) comprise entre un minima de 16,6 km/s, un maxima de 72,8 km/s.
On peut exprimer, en fonction de l’angle de direction par rapport à l’orbite, la variation de la vitesse supplémentaire par : V × (√2 − cos Â) = V∞ ⋅ Â désignant l’angle, cos son cosinus, pour 0° on obtient le coefficient (√2 − 1) = 0,4142… et pour 180°, (√2 + 1) = 2,4142.
Les vitesses permettent des formules simples, en unités SI et en prévision des démonstrations suivantes, la 3e vitesse cosmique, peut s’écrire, avec G (constante de la gravitation), M3 (masse du Soleil), m (masse de la planète), L (demi-grand axe), r (rayon) de la planète.

Pour  = 0°, (√2 − cos 0)2 = 0,17157, et après réduction au même dénominateur :

Les vitesses élevées au carré ont un sens physique de forces vives qui n’est pas évident dans l’expression de la 3e vitesse cosmique par les longueurs L et r. Cette formule équivalente, pour la Terre, à V32 = 11,182 + 12,342 = 16,652 a l’avantage de montrer que s’il existe des astromètres pour honnir les calculs d’un astrologue sur des “variables indépendantes” (rayon r, distance L), il n’est pas question, en astronomie appliquée (astronautique), d’ignorer les caractéristiques (masse, rayon) de la planète d’où l’on veut décoller. Même en prenant de l’altitude, les formules intègrent des variables (rayon + h) qui ne peuvent être indépendantes que chez les schizophrènes. En astronautique, il existe, bien entendu, un plus grand nombre de variables (notamment les perturbations) que celles prises en compte dans les formules ci-dessus.
On retiendra que pour quitter la surface d’une planète il faut ajouter une vitesse2 à la 1re vitesse cosmique, V12 = G ⋅ m / R. Pour changer théoriquement d’orbite, on ajoute ou on soustrait une V2, en relation avec l’orbite visée, à la vitesse2 circulaire de l’orbite délaissée. C’est donc d’une façon mathématiquement orthodoxe que la formule 2 ⋅ (V32 − 452) ou 2 ⋅ V32 − 63,632 permet de passer d’une vitesse circulaire du système d3 (tableau XXVIII) à une vitesse2 circulaire du système dg, puisque pour la même planète, 2 ⋅ V32 − 63,632 = Vg2. Pour se déplacer directement dans le groupe des distances, on note d’abord que la vitesse de 63,63 km/s est la vitesse circulaire moyenne d’un corps céleste (masse négligée) situé à dg→3 = 0,2191 UA du Soleil actuel. Avec l’inverse de ce nombre (1/0,2191 = 4,564) pour la commodité des calculs, on passe d’une orbite dg à une orbite d3 par :

et de d3 à dg :

Soit, les données dg du tableau XXV :
| Soleil U |
0,049 |
Jupiter |
0,105 |
Uranus |
0,232 |
| Vénus |
0,079 |
Mars |
0,134 |
Neptune |
0,251 |
| Mercure |
0,086 |
Saturne |
0,170 |
Pluton |
0,705 |
L’orbite 0,1666 ayant été choisie pour déplacer Mars, centre des deux groupes, on s’assure qu’en effet :

Appliquée aux autres orbites dg, la formule conduit aux valeurs d3 du tableau XXVIII sans lesquelles nous n’aurions pas connu la dernière hyperbole. S’il fallait déplacer Mars de 0,134 à 0,049 UA, au lieu de 4,56 le coefficient 1 / dg→3 serait de 33,35. Les amateurs de cosmogonie pourront calculer leurs coefficients de transfert par :

L’orbite départ est désignée par d0, l’arrivée par d1, inférieure ici à d0. Par les vitesses du tableau XXVIII on peut avoir la curiosité de calculer ce qu’il faut de vitesse2 supplémentaire pour passer de Vg2 de chaque planète à la vitesse2 circulaire de l’orbite 0,166, soit : 72,962 en km2/s2. En procédant par couples, de façon à avoir : d3 × d′3 = 0,1662 ou V32 × V′32 = cte4 = 72,964, on obtient les vitesses :
| Couple |
km/s |
| Soleil - Pluton |
62,25 |
| Vénus - Neptune |
62,60 |
| Mercure - Uranus |
63,50 |
| Jupiter - Saturne |
62,80 |
Valeurs voisines de la vitesse de 63,63 km/s, calculée pour le déplacement de Mars de 0134 à 0,166 UA. Cette distance 0,166 ou 1/6 a été retenue comme la valeur entière (nombre 6) la plus proche de la distance (en UA) correspondant à la période de révolution sidérale du Soleil à l’équateur. Pour une période T = 25,38 j, valeur moyenne actuellement admise, d3 = 0,169 UA.
L’intérêt astrologique de ce déplacement est dans la répartition binaire-ternaire qui s’en dégage, conformément au modèle R.E.T. déduit des significations planétaires. L’intérêt astrométrique est dans les angles qui déterminent cette répartition, dans l’homogénéité (par des voies anti-académiques) des périodes planétaires et solaire exprimables dans le même ordre de grandeur (les jours) comme les satellites des planètes et certaines étoiles pulsantes. Autre intérêt : le jumelage de ces périodes par les 25 j de la rotation équatoriale solaire. Le problème cosmogonique est devenu plus simple à exposer, plus difficile à résoudre.
On retourne aux rapports L / g ou g / L, au choix, par les vitesses2 ou les distances dg, en passant ou non par le système d3 qui a le mérite d’être organisé en secteurs R.E.T. de 40° chaque, à 1°,5 près.
Si l’on commence par les vitesses, il faut savoir que la proportion :
 soit :
soit :

équivaut à convertir la Vg2 de chaque planète en unités Mars (Vg72 =81,242) ou à multiplier 1 / dg (inverse de la distance) par la distance Mars (dg7 = 0,134 UA). On obtient le rapport ğ / L̆ de la planète en unités Mars (ğ7 / L̆7 = 1), en élevant cette expression à la 3e puissance :
 soit :
soit :

Le rapport ḡ7 / L̄7 de Mars en unités terrestres étant égal à 1/4, on passe des unités Mars ci-dessus aux unités Terre, en multipliant le coefficient 23 par 1/4. Soit 8 par 1/4 = 2, nouveau coefficient de la formule (3).
 soit :
soit :

La vitesse circulaire 81,24 de Mars Vg7 est prise dans le système dg, alors que les vitesses au numérateur sont prises dans le système d3 où la vitesse circulaire, à 0,166 UA, est de 72,96 km/s. Le rapport des deux vitesses étant égal à 81,24 / 72,96 = 1,115, pour rendre l’expression (3) homogène, on divise 2 par 1,115 à la puissance 6 (ordre de grandeur de V2 élevée au cube), soit 2 / 1,1156 = 1,049. D’où, l’expression correcte par les V32 :

Si les V3 ont été correctement calculées, les résultats restituent les données, aux décimales près, perdues dans les transformations arrondies. Plutôt que revenir en arrière en remontant par les mêmes chemins, autant sonder les voies inconnues. Celles de l’astrologie tracent des angles particuliers : des “Aspects”… divisions du cercle de 360° par des nombres entiers simples 1, 2, 3, 4 pour les Aspects majeurs ; des fractions composées d’additions ou de multiples de ces entiers pour les Aspects dits mineurs, tels que : 30°, 45°, 150°, 75°.
À partir des données dg du tableau XXV, en adoptant 0,166 comme cible et, par conséquent 4,56 comme coefficient de déplacement, les d3 non moyennées des quatre couples planétaires, conduisent sensiblement aux angles ci-dessous, pris au foyer F de l’hyperbole de la figure 16 :
| Soleil - Pluton |
79°,2 ± 1°,3 |
| Vénus - Neptune |
45°,4 ± 1°,2 |
| Mercure - Uranus |
39°,6 ± 0°,2 |
| Jupiter - Saturne |
20°,4 ± 1°,4 |
| Mars |
0° |
Les ‘+’ concernent Soleil, Vénus, Mercure, Jupiter, les ‘−’ leur symétrique.
Pour revenir à la source g dans la marge d’imprécision admissible de 2 à 3 % et rester dans la ligne d’une cosmogonie astrologique, il faut user de ces angles, des arcs équivalents (angle degré × 0,01745) ou de leurs lignes trigonométriques (cosinus, sinus, tangente, cotangente). Tout comme les groupes forment deux parties liées, l’un inverse de l’autre par rapport à Mars, il y a de fortes chances pour que ces angles ou leurs lignes, à l’intérieur de chaque groupe, forment également un système harmonique.
Prenons l’exemple des arcs. Selon les données ci-dessus, l’angle du Soleil (79°,2 + 1°,3 = 80°,5) se mesure en radian (π / 180°), 80°,5 × 0,01745 = 1,405, chiffre très proche de 1,4142 ou √2. On peut être tenté de partir de 81°,03 = √2 en radian, pour les valeurs moyennes. Ce qui entraînerait Mercure = √2/2 = 0,707 (arc de 40°,51) ; Jupiter = √2/4 = 0,354 (arc de 20°,26) ; Vénus = 1/∛2 = 0,794 (arc de 45°,48). En unités Mars (1 = 0,166) les d3 idéales deviennent :
| Planète |
d̆3 |
Planète |
d̆3 |
| Soleil |
0,477 |
Pluton |
2,096 a |
| Vénus |
0,704 |
Neptune |
1,420 b |
| Mercure |
0,735 |
Uranus |
1,360 c |
| Jupiter |
0,862 |
Saturne |
1,16 d |
| Mars |
1 |
Mars |
1 e |
Par définition, les d̆3 de Pluton, Neptune, Uranus, Saturne, sont les inverses (1 / d̆3) de Soleil, Vénus, Mercure, Jupiter, avec Mars = 1, constante de leurs produits. La marge d’incertitude des données, et aussi parce qu’il s’agit de moyennes, nous autorise à rechercher un modèle de relations harmoniques entre ces nombres.
Ainsi, avec a = 2,081 ; c = 1,359 ; d = 1,16 le groupe s’harmonise autour de 2 avec a ⋅ c = √8 ; a ⋅ b ⋅ c = 4 ; a ⋅ b ⋅ c ⋅ d ⋅ e = c5 = c ⋅ (b + b2) = c ⋅ (√2 + 2) ; a ⋅ d = 1 + √2. Pour ces relations, les données de a, b, c, d, sont plus précises que celles, arrondies, indiquées. Les recherches synthétiques sur les angles obtenus par les demi-grands axes L et ceux obtenus par les rapports L / g décideront ultérieurement du modèle le plus acceptable. En attendant, nous allons nous rabattre sur les fractions simples du cercle (2π ou 360°) en adoptant 1/18 pour Jupiter-Saturne (20°) ; 1/9 pour Mercure-Uranus (40°) ; 1/8 pour Vénus-Neptune (45°) ; 2/9 pour Soleil-Pluton (80°).
En négligeant momentanément le coefficient 1,049,

peut s’écrire :

Et, effectuant la partie numérique, il vient que :

Le rapport V32 / 72,962 d’une planète est égal au rapport d3 Mars (0,166) / d3 planète. Usant de l’avantage qu’offrent les nombres entiers, puisque 0,166 = 1/6… V32 / 72,962 se transforme en 1 / (6 ⋅ d3).
Mais, pour des raisons que seuls les sumériens et les astrologues comprendront, nous avons mis un point d’honneur à intégrer les angles à notre retour vers les gravités planétaires. Existe-t-il donc, pour tenir ce défi, une relation entre les angles, pris au foyer F, formés par l’axe des abscisses, et les rayons vecteurs Fp (à ne pas confondre avec les distances d3) ? Certes, oui… la relation existe, mais sa démonstration suppose des connaissances mathématiques qui, bien qu’élémentaires, paraîtront fabriquées et tortueuses aux astrologisants symbolistes. Lorsqu’un astrologue se réfère aux nombres, de leur côté, les anti-astrologiens se croient généralement obligés de réciter leur table de multiplication pour montrer qu’ils en savent plus long qu’eux. N’était-ce cette position de supériorité malveillante, je n’aurais pas eu à reformuler des acquis de culture générale pour certaines illustrations chiffrées. Cette fois, un exposé sur les théorèmes géométriques serait d’une aridité indigeste. Les lecteurs curieux d’analyse pourront soit consulter les ouvrages appropriés, soit écrire au COMAC. Les prévôts de la science retrouveront la relation d’eux-mêmes, comme j’ai pu le faire à partir des théorèmes trigonométriques et des propriétés des hyperboles équilatères. Elle transforme le rapport 0,166 / d3 en rapport des cosinus de l’angle au foyer ±  qui se dédouble en  / 2 + 22°,5 et  / 2 − 22°,5, Exemple, Pluton. Angle : −80°. Demi-angle −40°. On prend le rapport :

Le cosinus de −62°,5 = 0,4617, celui de −17°,5 = 0,9537. Le rapport des deux = 0,48416… qui conduit à une valeur d3 Pluton de : 0,344 (y, tableau XXX) au lieu de 0,342 UA, pour un angle F̂ de −79°,6. En calcul simplifié, pour avoir d3 on prend l’inverse du rapport des cosinus et on divise par 6.
Par définition, le produit x, y des coordonnées d’une hyperbole équilatère rapportée à ses axes, est égal à une constante k, 0,1662 ou 1/36, pour notre hyperbole. Si :
- d3 Pluton (y) × d3 Soleil (x) = 1/36,
- pour : d3 Pluton = 1 / (6 × 0,484) = y,
- alors : d3 Soleil = 0,484 / 6 = x.
En méthode abrégée, le calcul d’un seul rapport des cosinus (± Â / 2 ± 22°,5) suffit pour avoir les données x, y, de l’hyperbole équilatère. La géométrie démontre diverses relations entre les coordonnées x, y, transformées en X, Y par rotation de 45°. Notamment, et pour le plus simple : x + y = X ⋅ √2 ; x − y = Y ⋅ √2 parmi d’autres égalités possibles.
Pour traiter de ces relations sans littérature, les esthètes se laisseront séduire par les fonctions hyperboliques (cosh, sinh, tanh, coth) qui mettent en vedette le nombre e (2,718 28 à 10−5 près) déterminé par une sommation en série de 1/n ! (inverses de factorielles d’entiers simples). Nous reportons à une brochure plus concentrée un résumé strictement formaliste de ces recherches.
Article suivant — 2.5/2. Cosmogonies comparées
[1] Les constantes universelles. Gilles Cohen-Tannoudji. Hachette, 1991.
[2] Le système du monde : histoire des doctrines cosmologiques de Platon à Copernic (10 volumes). Pierre Duhem. Herman, 1959.
[3] Les hypothèses cosmogoniques. Alexandre Dauvillier. Éd. Masson, 1963.
[4] Diogène. Philosophie et Sciences Humaines. no 155. Gallimard, 1991.
[5] Les planètes naissent aussi, op. cit.
[6] Willy Benz. La Recherche no 228, 1991.
[7] Encyclopédie Atlas d’astronomie. Vol. 4. Chap. II. Éd. Atlas. Paris, 1984.
[8] Nombres et formes du cosmos, op. cit.
[9] La Grèce ancienne. I - Du mythe à la raison. Jean-Pierre Vernant, Pierre Vidal-Naquet. Seuil, 1990.