Introduction à la cosmogonie astrologique
 Ce livre est dédié aux mémoires oubliées des Sumériens, aux astronomes qui ont renié l’Homme, aux astrologues qui ont renié le Ciel.
“La réalité mathématique, de par sa structure, son harmonie interne, est une réserve inépuisable d’organisation. En choisissant au hasard des formules, on n’obtiendra de résonance entre elles, que si elles ont, ensemble, une certaine cohérence. Les mathématiques ont justement (...)
Ce livre est dédié aux mémoires oubliées des Sumériens, aux astronomes qui ont renié l’Homme, aux astrologues qui ont renié le Ciel.
“La réalité mathématique, de par sa structure, son harmonie interne, est une réserve inépuisable d’organisation. En choisissant au hasard des formules, on n’obtiendra de résonance entre elles, que si elles ont, ensemble, une certaine cohérence. Les mathématiques ont justement (...)
Lire la suite
1.1. Gravitation
 Organisation des demi-grands axes des orbites principales
Dans sa quête des fondements physico-harmoniques des préceptes astrologiques, l’astronome-astrologue Johannes Kepler (1571–1630) a découvert trois lois empiriques qui, sous leur forme simplifiée, s’énoncent ainsi :
▶ 1re loi (1609) : chaque planète décrit une orbite elliptique dont le Soleil occupe un des foyers.
▶ IIe loi (1609) : le rayon (...)
Organisation des demi-grands axes des orbites principales
Dans sa quête des fondements physico-harmoniques des préceptes astrologiques, l’astronome-astrologue Johannes Kepler (1571–1630) a découvert trois lois empiriques qui, sous leur forme simplifiée, s’énoncent ainsi :
▶ 1re loi (1609) : chaque planète décrit une orbite elliptique dont le Soleil occupe un des foyers.
▶ IIe loi (1609) : le rayon (...)
Lire la suite
1.2. Loi de Titius-Bode
 Organisation des demi-grands axes des orbites principales
Les distances moyennes au Soleil ou demi-grands axes varient, pour nos neuf planètes connues, de 0,387 UA (Mercure) à 39,44 UA (Pluton). En raison de leur excentricité, Mercure se rapproche du Soleil jusqu’à 0,31 UA, Pluton s’en éloigne jusqu’à 49 UA. Kepler a tenté d’intégrer dans des polyèdres emboîtés toutes les variations de distances (voir (...)
Organisation des demi-grands axes des orbites principales
Les distances moyennes au Soleil ou demi-grands axes varient, pour nos neuf planètes connues, de 0,387 UA (Mercure) à 39,44 UA (Pluton). En raison de leur excentricité, Mercure se rapproche du Soleil jusqu’à 0,31 UA, Pluton s’en éloigne jusqu’à 49 UA. Kepler a tenté d’intégrer dans des polyèdres emboîtés toutes les variations de distances (voir (...)
Lire la suite
1.3. Courbure des interdistances & progression par les angles
 Organisation des demi-grands axes des orbites principales
Insatisfait autant de Titius, de Bode que de Schmidt, j’ai commencé en 1961 mes propres investigations sur les distances. Puisque les significations planétaires se déduisaient des intervalles de temps, j’ai supposé que les écarts de distances, selon le même principe plutôt que la même formule, devaient être révélatrices d’une structure ignorée. (...)
Organisation des demi-grands axes des orbites principales
Insatisfait autant de Titius, de Bode que de Schmidt, j’ai commencé en 1961 mes propres investigations sur les distances. Puisque les significations planétaires se déduisaient des intervalles de temps, j’ai supposé que les écarts de distances, selon le même principe plutôt que la même formule, devaient être révélatrices d’une structure ignorée. (...)
Lire la suite
1.4. Des cotangentes aux entiers simples
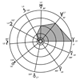 Organisation des demi-grands axes des orbites principales
S’il n’y avait que la géométrie sans la physique, l’axe de symétrie de la Fig. 5 se tracerait, en passant par le Soleil, de Pluton, 0°, à la longitude opposée, 180°. Les astéroïdes (184°) occupent cette position apparemment critique, et l’on peut chercher dans cet axe, non pas la symétrie du système, mais les raisons d’orbites mal conformées. (...)
Organisation des demi-grands axes des orbites principales
S’il n’y avait que la géométrie sans la physique, l’axe de symétrie de la Fig. 5 se tracerait, en passant par le Soleil, de Pluton, 0°, à la longitude opposée, 180°. Les astéroïdes (184°) occupent cette position apparemment critique, et l’on peut chercher dans cet axe, non pas la symétrie du système, mais les raisons d’orbites mal conformées. (...)
Lire la suite
1.5. Des entiers simples aux niveaux d’énergie
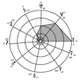 Organisation des demi-grands axes des orbites principales
Le lecteur averti aura reconnu dans la formule des cotangentes significatives pour le système solaire, un sérieux air de famille avec celle, découverte par Johann Jakob Balmer (1825–1898), physicien et ésotériste pythagoricien. Pour relier harmonieusement les longueurs d’onde des neuf raies alors connues du spectre d’émission de l’atome (...)
Organisation des demi-grands axes des orbites principales
Le lecteur averti aura reconnu dans la formule des cotangentes significatives pour le système solaire, un sérieux air de famille avec celle, découverte par Johann Jakob Balmer (1825–1898), physicien et ésotériste pythagoricien. Pour relier harmonieusement les longueurs d’onde des neuf raies alors connues du spectre d’émission de l’atome (...)
Lire la suite
1.6. Modèles solaires
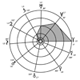 Organisation des demi-grands axes des orbites principales
Au milieu du siècle dernier, les physiciens Lord Kelvin et von Helmholtz, “assimilèrent le Soleil à une gigantesque sphère gazeuse se contractant lentement sous l’action de sa propre gravité. Ils pensaient qu’en se transformant en chaleur l’énergie gravitationnelle ainsi libérée par ce processus suffisait à maintenir le Soleil chaud et (...)
Organisation des demi-grands axes des orbites principales
Au milieu du siècle dernier, les physiciens Lord Kelvin et von Helmholtz, “assimilèrent le Soleil à une gigantesque sphère gazeuse se contractant lentement sous l’action de sa propre gravité. Ils pensaient qu’en se transformant en chaleur l’énergie gravitationnelle ainsi libérée par ce processus suffisait à maintenir le Soleil chaud et (...)
Lire la suite
1.7. Retour aux demi-grands axes
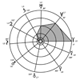 Organisation des demi-grands axes des orbites principales
La réduction d’un groupe de données, apparemment sans lien, à quatre fractions simples, nous instruit de la cohérence du système solaire. On pourrait s’abstenir de cerner la précision du retour aux données de départ, dès lors que la démonstration de leur interdépendance domine l’intérêt de leur précision. Néanmoins, ceux qui tiennent aux mesures (...)
Organisation des demi-grands axes des orbites principales
La réduction d’un groupe de données, apparemment sans lien, à quatre fractions simples, nous instruit de la cohérence du système solaire. On pourrait s’abstenir de cerner la précision du retour aux données de départ, dès lors que la démonstration de leur interdépendance domine l’intérêt de leur précision. Néanmoins, ceux qui tiennent aux mesures (...)
Lire la suite
1.8. Applications astrologiques
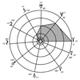 Organisation des demi-grands axes des orbites principales
“Nous avons dit que l’année d’un enfant de cinq ans lui semble longue parce qu’elle représente 1/5 de son existence, soit 0,20. L’année d’un homme de vingt ans lui semblera plus courte (1/20 de son existence, soit 0,05) dans le rapport de un à quatre. Celle d’un homme de cinquante ans ne vaudra plus que 1/50, soit 0,02. Le temps lui paraîtra (...)
Organisation des demi-grands axes des orbites principales
“Nous avons dit que l’année d’un enfant de cinq ans lui semble longue parce qu’elle représente 1/5 de son existence, soit 0,20. L’année d’un homme de vingt ans lui semblera plus courte (1/20 de son existence, soit 0,05) dans le rapport de un à quatre. Celle d’un homme de cinquante ans ne vaudra plus que 1/50, soit 0,02. Le temps lui paraîtra (...)
Lire la suite
2.1. Le r.e.t. dans le R.E.T.
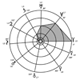 Demi-grands axes et gravités
Les trois régions du système solaire ne démentent pas l’association du R avec le proche, du T avec le lointain, du E avec le proche-lointain. Cette association de données objectives et subjectives est fidèle aux significations astrologiques parce que signaux et symboles communiquent : l’homme symbolise sa perception inconsciente du milieu qui l’habite, du monde qui vit (...)
Demi-grands axes et gravités
Les trois régions du système solaire ne démentent pas l’association du R avec le proche, du T avec le lointain, du E avec le proche-lointain. Cette association de données objectives et subjectives est fidèle aux significations astrologiques parce que signaux et symboles communiquent : l’homme symbolise sa perception inconsciente du milieu qui l’habite, du monde qui vit (...)
Lire la suite
2.2. Céphéides, étoiles pulsantes
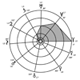 Demi-grands axes et gravités
Il y a de fortes chances pour que le rayon d’une planète résume l’histoire d’un équilibre conquis entre des forces antagonistes de cohésion et de rupture. Puisque l’organisation des orbites principales montre que les demi-grands axes ont subi des règles discriminatoires, on prend peu de risque à les étendre aux rayons stables des planètes du système solaire. On en prend un (...)
Demi-grands axes et gravités
Il y a de fortes chances pour que le rayon d’une planète résume l’histoire d’un équilibre conquis entre des forces antagonistes de cohésion et de rupture. Puisque l’organisation des orbites principales montre que les demi-grands axes ont subi des règles discriminatoires, on prend peu de risque à les étendre aux rayons stables des planètes du système solaire. On en prend un (...)
Lire la suite
2.3. D’oscillations en translations
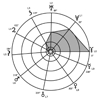 Demi-grands axes et gravités
Aucun astre ne se déplace dans l’espace à la manière d’un pendule de radiesthésiste ou d’une horloge à balancier. Or, de la formule simplifiée des mouvements planétaires se déduit, sans artifice, la formule tout aussi simple d’un mouvement pendulaire. Il faut être naïf ou avoir l’autorité des docteurs ès sciences pour oser le dire à l’occasion des étoiles pulsantes. Une autre (...)
Demi-grands axes et gravités
Aucun astre ne se déplace dans l’espace à la manière d’un pendule de radiesthésiste ou d’une horloge à balancier. Or, de la formule simplifiée des mouvements planétaires se déduit, sans artifice, la formule tout aussi simple d’un mouvement pendulaire. Il faut être naïf ou avoir l’autorité des docteurs ès sciences pour oser le dire à l’occasion des étoiles pulsantes. Une autre (...)
Lire la suite
2.4. Recentrage
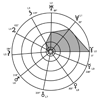 Demi-grands axes et gravités
Les périodes Tg sont supposées liées à une situation originelle d’oscillations ou translations. Ceci ne veut pas dire que l’absence de corps célestes aux distances correspondantes les prive de toute efficacité astrologique. Les rapports √(L / g), contemporains, organisés comme le modèle R.E.T. font la preuve du contraire. Au plan astrométrique, qui ne se dissocie pas de (...)
Demi-grands axes et gravités
Les périodes Tg sont supposées liées à une situation originelle d’oscillations ou translations. Ceci ne veut pas dire que l’absence de corps célestes aux distances correspondantes les prive de toute efficacité astrologique. Les rapports √(L / g), contemporains, organisés comme le modèle R.E.T. font la preuve du contraire. Au plan astrométrique, qui ne se dissocie pas de (...)
Lire la suite
2.5/1. Cosmogonies comparées
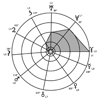 Demi-grands axes et gravités
La cosmologie concerne aussi bien le sacré que le profane, mais l’on peut faire une distinction de principe entre cosmogonie et cosmologie. La cosmogonie raisonne sur l’état véritable du monde, tandis que la cosmologie “est proprement une physique générale et raisonnée qui, sans entrer dans les détails trop circonstanciés des faits, examine du côté métaphysique les (...)
Demi-grands axes et gravités
La cosmologie concerne aussi bien le sacré que le profane, mais l’on peut faire une distinction de principe entre cosmogonie et cosmologie. La cosmogonie raisonne sur l’état véritable du monde, tandis que la cosmologie “est proprement une physique générale et raisonnée qui, sans entrer dans les détails trop circonstanciés des faits, examine du côté métaphysique les (...)
Lire la suite
2.5/2. Cosmogonies comparées
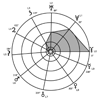 Demi-grands axes et gravités
Les angles 20°, 40°, 45°, 80° étant des angles approchés, pour compenser l’erreur prévisible entre l’angle réel et l’angle moyen, on peut soit adopter une formule de correction des angles, Â ± 1,5°, soit modifier le coefficient 1,049 de l’expression (4). Enfin, on peut comparer les résultats des deux solutions et choisir la plus avantageuse.
En élevant le coefficient initial de (...)
Demi-grands axes et gravités
Les angles 20°, 40°, 45°, 80° étant des angles approchés, pour compenser l’erreur prévisible entre l’angle réel et l’angle moyen, on peut soit adopter une formule de correction des angles, Â ± 1,5°, soit modifier le coefficient 1,049 de l’expression (4). Enfin, on peut comparer les résultats des deux solutions et choisir la plus avantageuse.
En élevant le coefficient initial de (...)
Lire la suite
Les canons du R.E.T.
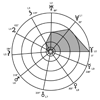 Demi-grands axes et gravités
La matrice-mère du R.E.T. (Fig. 19) a été conçue en 1959 à partir de la Théorie des âges et de la courbe (fragment d’hyperbole, Fig. 10) d’indice de vitesse de cicatrisation établie par Lecomte du Noüy. Ce modèle, qu’il aurait mieux valu appeler U.D.Q. (un, deux, quatre) ou U.D.M. (Unique, Duel, Multiple) en prévision des manipulations de langage qu’ont déjà suscité les termes (...)
Demi-grands axes et gravités
La matrice-mère du R.E.T. (Fig. 19) a été conçue en 1959 à partir de la Théorie des âges et de la courbe (fragment d’hyperbole, Fig. 10) d’indice de vitesse de cicatrisation établie par Lecomte du Noüy. Ce modèle, qu’il aurait mieux valu appeler U.D.Q. (un, deux, quatre) ou U.D.M. (Unique, Duel, Multiple) en prévision des manipulations de langage qu’ont déjà suscité les termes (...)
Lire la suite
Exoplanètes et système solaire
 L’Univers n’a peut-être pas la forme d’une boule de cristal — on s’interroge sur sa forme — mais les astrophysiciens y lisent des choses stupéfiantes sur les systèmes solaires qui ne sont pas d’ici et sur leur formation. Elle peut nous éclairer sur la notre. De leur plongée dans le passé surgissent les photos d’enfance de nos parents cosmiques : des étoiles, des couples d’étoiles qui engendrent des (...)
L’Univers n’a peut-être pas la forme d’une boule de cristal — on s’interroge sur sa forme — mais les astrophysiciens y lisent des choses stupéfiantes sur les systèmes solaires qui ne sont pas d’ici et sur leur formation. Elle peut nous éclairer sur la notre. De leur plongée dans le passé surgissent les photos d’enfance de nos parents cosmiques : des étoiles, des couples d’étoiles qui engendrent des (...)
Lire la suite
Réponse à un Mouchassieux
 S’il vous est arrivé de lire une Histoire de l’astronomie revue et corrigée par un astronome contemporain vous comprendrez qu’il n’y a aucune tolérance à espérer des tentatives d’explicative de l’astrologie par l’astrométrie. Question de territoire : impossible de douter du dogme ; en cas d’erreur on verra plus tard. Ainsi l’histoire des sciences à usage scolaire est présentée comme une évolution sans (...)
S’il vous est arrivé de lire une Histoire de l’astronomie revue et corrigée par un astronome contemporain vous comprendrez qu’il n’y a aucune tolérance à espérer des tentatives d’explicative de l’astrologie par l’astrométrie. Question de territoire : impossible de douter du dogme ; en cas d’erreur on verra plus tard. Ainsi l’histoire des sciences à usage scolaire est présentée comme une évolution sans (...)
Lire la suite
Tous droits réservés.
© 2003–2025
Richard Pellard. Reproduction interdite.
Webmestre :
Julien Rouger
AstroAriana — Site réalisé avec
SPIP