L’Univers n’a peut-être pas la forme d’une boule de cristal — on s’interroge sur sa forme — mais les astrophysiciens y lisent des choses stupéfiantes sur les systèmes solaires qui ne sont pas d’ici et sur leur formation. Elle peut nous éclairer sur la notre. De leur plongée dans le passé surgissent les photos d’enfance de nos parents cosmiques : des étoiles, des couples d’étoiles qui engendrent des planètes comme nos géniteurs gazeux du système solaire l’ont fait. On finira, c’est écrit dans le ciel, par savoir comment, en accumulant les photographies (rougies ?) du passé, les modèles, les statistiques et les idées ou rêveries qui en découlent.
Dans cette traque du passé, équivalent en référentiel “Objet” au subjectif “Qui sommes nous, d’où venons nous, ou allons-nous”, les exoplanètes font la “Une” des articles étourdissants.
Le site Encyclopédie du Savoir Relatif et Absolu [1] donne une brève définition (article de Franck Hecht) des exoplanètes :
Exoplanètes : Une exoplanète entendue également sous le nom de “Planète extrasolaire” n’est rien d’autre qu’une planète en-dehors de notre système solaire. Cependant, on préfère toujours donner le nom “étoile” quand on parle de ces planètes.
Le “cependant” est de trop. Les exoplanètes ont acquis un statut indépendant de l’étoile, leur Soleil, autour de laquelle elles gravitent. Les sites, tel celui du COMAC, ne se renouvellent guère. Celui du Savoir relatif et absolu… fait état des découvertes d’exoplanètes au 13 août 2000. Une cinquantaine d’exoplanètes sont recensées. Majoritairement, les périodes de révolution sidérale sont de l’ordre de trois jours, la demi-semaine, la semaine, le mois, rarement l’année [2].
Les extrasolaires sont immatriculées. Je ne connais pas la règle de codification, mais voici des exemples : HD 83443c… HD 75289… HD 202206. En privant les planètes de patronymes mythologiques les astronomes ôtent aux astrologues la possibilité d’en déduire aussitôt les “effets” et significations comme ils l’ont fait pour Uranus, Neptune, Pluton avec des a priori mythiques que les conditionalistes ont rectifié par l’observation et la théorie.
Il y a une exception récente dans les immatriculations : l’exoplanète HD 209458b qui tourne autour de l’étoile (1,05 de la masse solaire) HD 209458b a été baptisée Osiris en souvenir du dieu d’Égypte mutilé, car “surchauffée par la très grande proximité de son étoile” [3] son atmosphère d’hydrogène s’évapore au rythme de 10 000 tonnes par seconde.
Premier point : dans Nombres et Formes du Cosmos (1971), puis dans Éléments de cosmogonie astrologique [4] et de nombreux articles avant et après cette parution, j’ai démontré que l’on pouvait formellement obtenir les demi-grands axes actuels des planètes principales avec les formules des niveaux d’énergie de l’atome d’hydrogène [5]. Les écarts entre les calculs et les données sont inférieurs à 1 %. Dans les essais d’Éléments de cosmogonie, partant du modèle du R.E.T. combinant l’unique, le binaire, le multiple, j’ai énoncé l’hypothèse d’une masse originelle unique de laquelle une masse partielle se détache pour engendrer un système planétaire par ses interactions avec l’étoile dont elle procède.
En détachant une masse partielle de la principale, en binaire par unique dédoublé, le couple crée ses planètes par interactions gravifiques et interférences “ionisantes”. Cette hypothèse est la plus conforme aux représentations géométriques induites par les données traitées (coniques à deux foyers). Elle justifie les couples en symétries et l’existence d’un plan médian séparateur. Les masses de Jupiter et Saturne, ainsi qu’on l’admet communément, seraient les premiers et principaux vestiges d’un méga-astre initial, compagnon-satellite du Soleil. Selon les distances actuelles, le plan médian passe dans la zone des astéroïdes [6].
Ce schéma n’interdit pas l’intermède des anneaux au sein desquels se produisent les accrétions prédominantes dans des directions privilégiées comme le laisse supposer le bras de spirale formé par les rapports consécutifs des demi-grands axes et leurs relations avec les niveaux d’énergie de l’hydrogène. Ce “détail” majeur est encore absent des modèles officiels :
“Les grandes lignes du scénario de formation des planètes semblent maintenant relativement bien comprises ; elles reposent sur la condensation et l’agglomération de grains de glace poussiéreux solides qui peuvent grossir jusqu’à une dizaine de masses terrestres. La proto-planète qui atteint ce stade peut alors croître rapidement en captant par gravité le gaz situé dans l’anneau qu’elle parcourt autour de son étoile. On comprend pourquoi les planètes géantes sont éloignées du Soleil : tout simplement parce qu’il n’y a pas assez de matière dans un anneau proche du Soleil et parce que la glace ne peut pas rester solide en deçà de quelques unités astronomiques du Soleil”… [7]
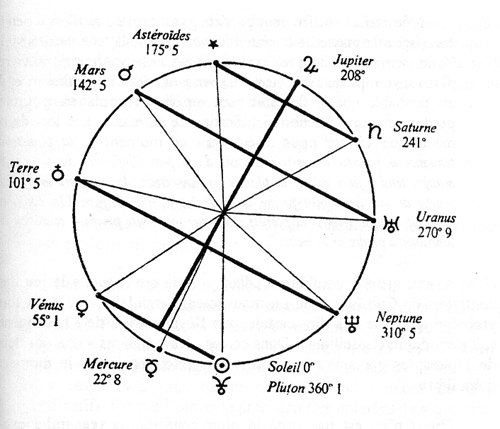
L’hypothèse des directions privilégiées remonte à Nombres et Formes du Cosmos (1971) avec le modèle d’un corps céleste dont le rayon, tel celui d’une Céphéide, se dilate et se rétracte. J’ai abandonné partiellement ce modèle au profit des anneaux. Autre détail absent des scénarios officiels : les couples planétaires de Vénus à Pluton, sensiblement symétriques et leur constance moyenne de 5,32 UA [8]. Ces symétries ont illustré plusieurs de mes articles. Je reproduis, à l’intention des jeunes et nouveaux conditionalistes, la figure de Pour une astrologie moderne [9] qui fait apparaître les couples planétaires, la séparation par l’axe Jupiter-Mercure entre planètes telluriques (non gazeuses, denses, peu massives, proches du Soleil) et planètes géantes (gazeuses, peu denses, massives, lointaines). À l’occasion de cette figure, je me suis permis d’observer que Pluton, en revenant dans l’axe 0°–180° de la figure rejoignait les telluriques en se plaçant dans le vis-à-vis des astéroïdes (Cérès). Une vision globale du système solaire, trop primaire pour séduire des scientifiques.
Une belle photo d’Isis en noir et blanc trône dans ma bibliothèque. Je n’ai pas celle d’Osiris son époux, mais j’incline à croire que ce dieu et sa planète protègent le conditionalisme. C’est la première fois, en 2003, qu’une “atmosphère d’hydrogène dense, chaude et extrêmement étendue” a été observée autour d’une planète hors du système solaire. L’équipe de l’IAP [10] (Institut d’Astrophysique de Paris) responsable de cette observation ne savait pas qu’elle allait cautionner un modèle d’organisation des orbites planétaires fondé sur les niveaux d’énergie de l’hydrogène… répandu mais pas perdu par Osiris qu’Isis a reconstitué ensuite, selon le mythe. Un mythe adapté à une atmosphère évaporée puis recondensée en planètes distinctes.
La symétrie des couples planétaires est ignorée ou non-mentionnée. En revanche, toujours grâce à Osiris, on comprend mieux le processus qui peut conduire à la bipartition des planètes, telluriques d’un côté, gazeuses de l’autre. L’exoplanète perd 10 000 tonnes d’hydrogène par seconde. Énorme ? Non, ce n’est “rien” :
“Même si ce chiffre peut paraître gigantesque, ce n’est ‘rien’ comparé à la masse de la planète ; à ce rythme-là, elle perdrait 0,1 % de sa masse en cinq milliards d’années ; elle pourrait donc vivre plus longtemps que son étoile. Cependant, c’est un minimum et il est probable que le flot soit bien supérieur ; la planète pourrait perdre ainsi une fraction significative de sa masse. Les lois de la mécanique céleste nous disent qu’à ce moment-là, la planète a tendance à repartir en arrière. Ainsi, d’une part l’influence du disque de matière tend à faire migrer la planète vers son étoile, d’autre part la planète proche de son étoile peut perdre de la masse et s’en éloigner. Un équilibre pourrait donc se créer et la planète rester sur son orbite proche à condition de continuer à perdre de la masse.” [11]
Avant, arrière, équilibre médian… voilà qui rappelle le jeu des contraires de C.-G. Jung… ou un mouvement pendulaire, car il est fort probable, pour ne pas dire certain, que l’évaporation de l’hydrogène soit périodique et oscillante. Dans ce cas : les “arrières” sont au-delà de Jupiter, les “avants” en deçà… et Jupiter représente le moment d’équilibre.
Osiris n’en est pas resté là pour conforter la recherche exo-académique. Nous lui devons une plus belle chandelle. En effet, (et je souligne) :
“Ce phénomène d’évaporation des planètes trop proches de leur étoile pourrait ainsi expliquer l’absence de planètes à moins de sept millions de kilomètres de leur étoile [soit, 0,047 UA]”, concluent Alfred Vidal-Madjar et ses collègues : “ces planètes doivent s’évaporer très rapidement, ou devenir des planètes moins massives et pauvres en hydrogène, comme Neptune, ou même ne plus montrer que leur cœur solide mis à nu”. [12]
Autrement dit, une étoile imposerait un désert brûlant, sans planète possible jusqu’à une distance autour de 0,047 UA. Ainsi, Osiris gravite autour de son étoile en 3,52 jours, à la distance désignée.
Deuxième point : dans Éléments de Cosmogonie, comme première distance obtenue par la moyenne géométrique des demi-grands axes et par l’intensité actuelle de la gravité à la surface du Soleil, j’indique : 0,049 UA et une période de 3,93 jours résultant de la formule (cf. note 1) du pendule simple :

Avec :
- Tg : période d’oscillation
- L : longueur du pendule (ici, une distance)
- g : intensité de la gravité où bat le pendule (ici le rayon moyen d’une étoile ou d’une planète).
Les données terrestres, avec L : 150 000 000 km = 1,5 × 1011 m et g = 9,8 m/s2, donnent, en secondes, sensiblement l’équivalent de 9 jours. Pour les autres calculs, en exprimant les distances L̄ en UA, la gravité moyenne ḡ en unités terrestre (9,8 m = 1), il suffit de multiplier la racine du rapport L̄ / ḡ par 9 jours pour avoir les périodes Tg respectives sans passer par un grand nombre de chiffres significatifs. Ce que l’ordre de précision (les données de g sont des moyennes) n’exige pas.
Les résultats sont aussi étonnants que l’idée d’appliquer la formule du pendule simple aux planètes et à leurs gravités [13]. Bien que cette idée soit déjà venue à l’esprit de Galilée et Mikhaïl Vassilievitch Lomonossov [14] dans des perspectives différentes, l’application formelle que j’en ai faite est inédite. Les résultats le sont également. Ils font ressortir un ordonnancement conforme à un modèle astrologique, le R.E.T., incompréhensible, par conséquent irrecevable, pour les modèles qui ont le label de scientifique (celui de “bio” nous reviendra).
Selon ce qui précède, afin de déterminer la période Tg du Soleil j’ai posé la formule :

Une période Tg pendulaire qui correspond dans le système solaire à la distance d’un astre qui graviterait autour du Soleil actuel à la distance, en UA, de 0,049 UA. Celle d’Osiris est de 0,047 UA et je pourrais m’offrir le luxe, jusqu’à plus ample informé, que le rapport entre 0,049 et 0,047, égal à 1,043 est proche du rapport des masses de l’étoile d’Osiris et de celle de notre Soleil : 1,05.
L’intensité de la gravité du Soleil à la surface (rayon moyen) est 27,9 fois 9,8 m/s2 (valeur de g moyen de la Terre). La distance de 5,32 UA demande de revenir aux données du tableau de la page suivante, publié dans les Éléments, non révisé depuis, les précisions au-delà de la 4e, voire de la 2e décimale étant superflues.
À partir de ces données, on calcule les produits des demi-grands axes des couples :
| Vénus - Pluton |
28,51 = 5,34 × 5,34 = 5,342 |
| Terre - Neptune |
30,11 = 5,49 × 5,49 = 5,492 |
| Mars - Uranus |
29,27 = 5,41 × 5,41 = 5,412 |
| Cérés - Saturne |
26,47 = 5,14 × 5,14 = 5,142 |
| Jupiter |
27,06 = 5,20 × 5,20 = 5,202 |
Tableau — Données des planétaires principales (Cérès pour les astéroïdes). Distances en UA.
| Excentricité |
Planète |
Distance
périhélie (UA) |
Distance
aphélie (UA) |
Demi-grand
axe (UA) |
| 0,2056 |
Mercure |
0,308 |
0,466 |
0,387 1 |
| 0,0068 |
Vénus |
0,718 |
0,729 |
0,723 3 |
| 0,0167 |
Terre |
0,983 |
1,017 |
1 |
| 0,0933 |
Mars |
1,382 |
1,666 |
1,523 7 |
| 0,077 |
Cérès |
2,557 |
2,983 |
2,77 |
| 0,0483 |
Jupiter |
4,951 |
5,454 |
5,202 6 |
| 0,0559 |
Saturne |
9,02 |
10,089 |
9,554 7 |
| 0,0463 |
Uranus |
18,328 |
20,108 |
19,218 1 |
| 0,009 |
Neptune |
29,839 |
30,381 |
30,109 6 |
| 0,2486 |
Pluton |
29,634 |
49,243 |
39,438 7 |
La moyenne géométrique des couples de Vénus-Pluton à Cérès-Saturne est égale à 5,34 UA. Valeur proche de 5,20 UA, demi-grand axe de Jupiter qui se suffit à lui-même. Ces calculs sont conformes aux symétries de la figure obtenue par les rapports [15] consécutifs des demi-grands axes. Si l’on prend deux décimales après la virgule, la moyenne tombe à 5,32 UA. En poussant les décimales jusqu’à la 4e, on n’excédera pas 5,34 UA. Par prudence autant que par sagesse, je signale que Cérès est le plus important des astéroïdes. En outre, l’orbite brisée des astéroïdes s’étendant entre 2,17 et 3,3 UA, la moyenne géométrique de ces deux nombres donne 2,67 UA.
Avec 5,32 ou 5,34 UA, nous sommes dans la marge acceptable de l’orbite de Jupiter. Un supplément au demi-grand axe (5,20 UA) entre 2 et 3 %, en deçà de la distance de son aphélie (5,45 UA).
Avec la 3e loi de Kepler [16], on déduit, en unités terrestres de 1 an et 1 UA, les périodes des révolutions sidérales. Cette loi ne s’applique ni aux distances des périhélies, ni aux distances des aphélies. Cependant, il est intéressant de tester les produits des mêmes couples et juger indirectement de l’impact des excentricités.
Produits des distances aux périhélies :
| Vénus - Pluton |
21,28 = 4,61 × 4,61 = 4,612 |
| Terre - Neptune |
29,33 = 5,42 × 5,42 = 5,422 |
| Mars - Uranus |
25,33 = 5,03 × 5,03 = 5,032 |
| Cérès - Saturne |
23,06 = 4,80 × 4,80 = 4,802 |
| Jupiter |
24,51 = 4,95 × 4,95 = 4,952 |
Curiosité récompensée : la moyenne géométrique des distances aux périhélies de Vénus à Pluton est égale à 4,96 UA, soit le périhélie de Jupiter (4,951 UA).
Produits des distances aux aphélies :
| Vénus - Pluton |
35,90 = 5,99 × 5,99 = 5,992 |
| Terre - Neptune |
30,99 = 5,56 × 5,56 = 5,562 |
| Mars - Uranus |
33,50 = 5,79 × 5,79 = 5,792 |
| Cérès - Saturne |
30,09 = 5,49 × 5,49 = 5,492 |
| Jupiter |
29,75 = 5,45 × 5,45 = 5,452 |
La moyenne géométrique des distances aux aphélies, de Vénus à Pluton est égale 5,70 UA ou 5,65 si l’on intègre l’aphélie de Jupiter à ce calcul.
Avec les trois valeurs de chaque couple de planètes obtenues de leurs produits : périhélie, demi-grand axe, aphélie, il est possible de construire quatre ellipses aux dimensions comparables entre elles, ainsi qu’avec celle que donnent les moyennes géométriques des orbites actuelles, voisine de l’orbite réelle de Jupiter. Pour cette résultante, l’ellipse ayant un demi-grand axe de 5,34 UA, un périhélie de 4,96 UA et un aphélie de 5,70 UA, entraîne une distance focale de 0,37 UA, valeur proche du demi-grand axe de Mercure (0,387 UA). Ce n’est peut-être qu’une coïncidence mais, en matière de recherches marginales, c’est-à-dire ailleurs que là où on ne cherche pas, aucune coïncidence n’est à négliger. Avant que Newton en donne une justification physique provisoire, la 3e loi de Kepler pose une égalité bizarre entre une surface temporelle (T2) et une distance de dimension volumique (D3). Imaginez une heure d’attente dans une gare transformée en un carré géométrique de 60 minutes × 60 minutes, et que cette surface soit égale au volume d’une très petite sphère ou d’un cube. Votre imagination vous aura piégé. Parce que le temps linéaire d’une attente n’a rien à voir avec le temps circulaire d’une révolution sidérale qui introduit des vitesses et des accélérations, tout comme le volume, en physique et non en géométrie pure, conduit à la masse, la densité d’un corps. Il n’y a pas beaucoup d’ouvrages de vulgarisation qui expliquent comment et pourquoi la 3e loi de Kepler, qui n’était qu’un constat de relation “harmonieuse” entre le temps et l’espace, est rentrée dans l’ordre de la logique et des grandeurs physiques fondamentales (masse, longueur, durée) grâce à Newton et à la constante G. J’ai signalé l’ouvrage que je connais [17].
“Les planètes extra-solaires connues sont radicalement différentes de ce qu’on attendait” écrit Roger Ferlet. Les théoriciens prévoyaient des planètes de périodes de l’ordre 10 ans, massives, gazeuses, sensiblement aussi éloignées de leur étoile que notre Jupiter. Osiris les a confondus : les exoplanètes sont majoritairement massives, gazeuses mais proches de leur étoile, “…jamais (à une exception près) à moins de 0,04 UA.” C’est pourquoi, écrit Roger Ferlet :
“Les exoplanètes les plus proches de leur étoile sont surnommées les ‘Jupiter chauds’. Nous avons vu qu’elles n’ont pas pu se former où on les trouve. Alors pourquoi donc ont-elles des périodes aussi courtes ? La réponse avait déjà été trouvée par deux théoriciens avant la découverte de 51 Pégase ! [18] Lorsqu’une planète a accrété tout le gaz dans l’anneau qu’elle parcourt autour de son étoile, elle ne grandit plus, mais sa masse perturbe le disque de matière qui, en retour, perturbe l’orbite de la planète. Et en un temps de l’ordre de 100 000 ans (ce qui est court par rapport au temps de formation de la planète), la planète migre vers l’étoile.”
Il y a quinze ans, deux théoriciens avaient donc imaginé la migration d’une proto-planète d’une orbite éloignée à une distance limite près de son étoile. Dans les Éléments de Cosmogonie, avec la moyenne de huit orbites et la masse du Soleil, réunissant l’ensemble du système, j’ai suggéré une migration de sens inverse, du proche au lointain, d’Osiris à Jupiter.
Pour démolir ces corrélations, il est difficile de s’en prendre aux produits des orbites. En revanche, l’incongruité de pendules de longueurs égales aux distances astronomiques des demi-grands axes prête flanc à la critique… si l’on associe le terme de “pendule” à la représentation concrète d’un fil reliant une planète au Soleil. On évite ce genre de figure en employant le terme plus général “d’oscillateur harmonique”. La formule ne change pas, mais la visualisation courante d’une boule suspendue oscillant de droite à gauche, gauche à droite, est écartée : un ressort qui se tend et se détend périodiquement, un ballon qui se gonfle et se dégonfle, tel une étoile “Céphéide”, sont des oscillateurs harmoniques. Dans ma Réponse à un Mouchassieux, j’ai démontré comment passer de la formule du pendule simple à celle de la densité d’un tore ayant pour section le rayon moyen de la planète.
a) Formule du pendule :

b) g moyen, à la surface, étant égal à :

avec G (constante de la gravitation), m (masse de la planète), r (son rayon moyen).
La formule (1) devient :

Son inverse ou fréquence au carré :

c) Le volume V d’un tore de section r, de circonférence 2π ⋅ L est égal à :

d) La masse volumique ρ étant égale au quotient m / V, la formule (5) devient :

(à diviser par 1000 pour avoir la densité par rapport à celle de l’eau).
e) On obtient la même formule en divisant 1 / Tg2 par G / 2.
Du pendule transformé en densité d’un tore, il apparaît que la période Tg est proportionnelle à la racine carrée de l’inverse de la densité. Si ρ = 2 / (G ⋅ Tg2) alors Tg ∝ 1 / √ρ et le coefficient de proportionnalité pour Tg2 ∝ 1 / ρ devient G / 2. Soit :

La relation entre le temps et la densité est conforme aux théories cosmologiques (cf. Réponse à un Mouchassieux) et il est des astronomes autres qu’un Mouchassieux qui se sont étonnés de trouver la formule « connue des oscillations du pendule » liée à la densité moyenne d’une sphère, telle qu’une étoile pulsante (je souligne) :
Dans le cas le plus simple des pulsations d’une sphère homogène la période des oscillations Π3 est liée à la densité moyenne de la sphère ρ3 par la relation :

(où ρ3 est en kg ⋅ m−3 et γ est le rapport des chaleurs spécifiques pour le matériau stellaire, soit 5/3 pour un gaz monoatomique.)
Il est curieux que cette expression se déduit de la formule connue des oscillations d’un pendule, si au lieu de la longueur l’on y porte le rayon de l’étoile (R) et si on tient compte de l’accélération de la pesanteur à la surface de l’étoile :

(Astronomie. M. Dragrev, V. Demine, I. Klichine, V. Tcharouguine. Éditions MIR. Moscou. 1983).
Depuis Newton et sa synthèse des lois de Kepler par la mathématique de la mécanique céleste, la relation entre le demi-grand axe d’une planète (que je désigne par L), sa masse m (négligeable devant celle du Soleil), sa révolution sidérale T ou P selon les auteurs, la constante universelle G et la masse du Soleil M3 s’écrit :
f)

ou en négligeant m :

dont on obtient en effectuant le remplacement, une formule applicable à toutes les planètes en révolution autour du Soleil :

avec :

g) de la formule (8) découle la masse du Soleil :

h) tout comme de la formule (3), pour la période Tg du pendule découle la masse de la planète :

i) le rapport M3 / m égal à G ⋅ M3 / (G ⋅ m) devient :

j) on porte G ⋅ m au numérateur de la partie droite et L2 au dénominateur de la partie gauche :

k) G ⋅ M3 / L2 = accélération f3 exercée par le Soleil sur la planète à la distance L.
G ⋅ m / r2 = g, intensité moyenne de la gravité (autre accélération centrale) à la surface de l’astre de rayon r (moyen).
D’où :

Ou :

Ou la proportion :

l) On isole l’intrus Tg2 pour avoir sa formule à partir des données connues, sans passer par l’image (repoussante) d’un pendule physique :

Rappel : partout où il est question de la densité ρ, il faut diviser le résultat du calcul m / V (masse sur volume) par 1000 pour ne pas se faire taper sur les doigts par un Mouchassieux et avoir la densité par rapport à l’eau telle qu’on l’exprime dans les ouvrages d’astrométrie. Par rapport aux démonstrations des professionnels, les formules de (1) à (13) sont simplifiées, par rapport aux articles de vulgarisation, elles sont compliquées. En choisissant l’entre-deux, les spécialistes me trouveront incomplet et les non-initiés incompréhensible. C’est le sort réservé à la fonction “Mars” et je me flatte de la vivre entièrement, car elle est au centre du R.E.T. Il n’y a d’équilibre qu’au centre (Hara) qu’est l’engagement.
Il s’agit bien d’une période intruse ; pour un astronome, sans théorie explicative, elle n’a pas de sens. Or, outre Osiris pour le Soleil et l’ensemble du système, les résultats classent les planètes par couples différents de ceux qui mettent Jupiter en vedette, mais parfaitement cohérents avec un modèle astrologique (R.E.T. ou Logoscope) qui, avec la formule G ⋅ Tg2 transformant la période Tg2 en 1 / ρ, devient conforme à un classement des densités des tores planétaires. Une voie pour passer de l’astrologie symboliste à l’astrologie naturelle. Une autre voie intéressante est celle de la formule (13) : f3 ⋅ T2 = g ⋅ Tg2. Elle suggère un équilibre entre un potentiel (g ⋅ Tg2) et un réel (f3 ⋅ T2) ou une réaction de l’un à l’autre. Je me réserve d’en développer les possibilités dans de futures mises à jour, car je ne crois pas qu’il y aura, avant longtemps, un astronome pour jeter un regard compatissant ou cynique sur une recherche marginale. Les “savants ne sont pas curieux” a écrit Anatole France. L’astrophysicien qui surmontera sa répugnance pour voir ce qu’il y a derrière les symétries des périodes Tg, la formule qui permet de trouver les gravités moyennes respectives, s’engagera malgré lui, dans un commencement d’explicative de l’astrologie naturelle.
Pour ma part, j’ai suggéré trois directions d’interprétation physique :
▶ 1. Hypothèse osée : les résultats sont conformes à un état originel du système solaire.
▶ 2. Hypothèse positiviste : aucune référence à un état originel. Les résultats ne sont pas à interpréter. Ils expriment un état sous-jacent à l’état réel.
▶ 3. Hypothèse combinée : 1) est devenu 2) en laissant des traces. Un paramètre supplémentaire, une lecture différente de la formule du pendule rendent compte d’un aspect inconnu du système solaire contemporain.
La découverte d’Osiris et ses conséquences favorisent l’hypothèse combinée que ne démentirait pas Frédéric Guérin, auteur du texte qui suit, extrait du journal du CNRS (site sur Internet) :
“Ce qui se trame sur HD 209458b, Osiris, ressemble un peu à ce qu’a connu la Terre après sa naissance il y a 4,55 milliards d’années lorsque le Soleil brillait de ses pleins feux…”
Article paru dans le n° 29 des Cahiers conditionalistes (4e trimestre 2004).
Article suivant — Réponse à un Mouchassieux
[1] Il suffit sur Internet de taper “exoplanète” pour avoir, avec un moteur de recherche, la liste des articles, débats, découvertes, sites, concernant nos sœurs lointaines.
[2] J’ai connu un âne-adepte qui m’a demandé pourquoi, plutôt qu’en jours, je n’exprimais pas en secondes les périodes déduites des rapports L / g et de la formule du pendule simple. L’unité se choisit selon l’ordre de grandeur. Pourquoi exprime-t-on un âge en mois et en années, et non pas en secondes ou micro-secondes ? Parce que les unités choisies permettent d’être simple et de circonscrire une dimension du temps entre ses limites minimale et maximale.
[3] L’Astronomie. Mai 2003. (Bulletin de la Société Astronomique de France). Article de Roger Ferlet : Osiris, une exoplanète à l’allure de comète.
[4] Éléments de cosmogonie astrologique. COMAC. 1992.
[5] Ce qui a fait dire à un autre Cadichon que je prenais les planètes pour des électrons. On voit combien les astrologues sont ouverts à la recherche conditionaliste.
[6] Éléments de Cosmogonie. COMAC.
[7] L’Astronomie. Mai 2003. Article de Roger Ferlet.
[8] Unité astronomique et distance de la Terre au Soleil, généralement arrondie à 150 millions de km.
[9] Pour une astrologie moderne. Éd. du Seuil. 1977.
[10] Équipe de l’IAP : Alfred Vidal-Madjar, Alain Lecavalier des Étangs, Jean-Michel Désert et Guillaume Hébrard.
[11] L’Astronomie. Opus cité. C’est moi qui souligne.
[12] Commentaire relevé sur le site Yahoo Actualités. Sciences.
[13] Pour devancer la critique, j’ai calculé les gravités par la formule, en unités terrestres, rayon moyen × densité moyenne = g.
[14] Cf. Cahiers Conditionalistes no 29. Réponse à un Mouchassieux.
[15] Rappel : rapports pris pour des sinus et transformés en angles dont on fait la sommation.
[16] Dans les articles de vulgarisation, la 3e loi de Kepler se présente par L̄3 = T̄2 ou L̄3 / T̄2 = 1, avec L̄ = demi-grand axe en U.A. et T̄ = révolution sidérale en années. En unités S.I. (système international) en tenant compte de la masse (m) de la planète et avec M3 pour celle du Soleil on a L3 / T2 = G ⋅ (M3 + m) / 4π2. Longueur ou distance en mètres, T en secondes, M3 et m en kg.
[17] Les constantes universelles. Gilles Cohen Tannoudji. Hachette. 1991.
[18] Première détection d’une planète extra-solaire, autour de l’étoile 51 Pégase. “La théorie prévoyait des planètes de périodes de l’ordre de dix ans alors que les mesures donnaient une période de 4,2 jours pour 51 Peg !” (R. Ferlet. article cité).

Pluton planète naine : une erreur géante
par Richard Pellard
117 pages. Illustrations en couleur.
Pluton ne fait plus partie des planètes majeures de notre système solaire : telle est la décision prise par une infime minorité d’astronomes lors de l’Assemblée Générale de l’Union Astronomique Internationale qui s’est tenue à Prague en août 2006. Elle est reléguée au rang de “planète naine”, au même titre que les nombreux astres découverts au-delà de son orbite.
Ce livre récapitule et analyse en détail le pourquoi et le comment de cette incroyable et irrationnelle décision contestée par de très nombreux astronomes de premier plan. Quelles sont les effets de cette “nanification” de Pluton sur son statut astrologique ? Faut-il remettre en question son influence et ses significations astro-psychologiques qui semblaient avérées depuis sa découverte en 1930 ? Les “plutoniens” ont-ils cessé d’exister depuis cette décision charlatanesque ? Ce livre pose également le problème des astres transplutoniens nouvellement découverts. Quel statut astrologique et quelles influences et significations précises leur accorder ?
Enfin, cet ouvrage propose une vision unitaire du système solaire qui démontre, chiffes et arguments rationnels à l’appui, que Pluton en est toujours un élément essentiel, ce qui est loin d’être le cas pour les autres astres au-delà de son orbite. Après avoir lu ce livre, vous saurez quoi répondre à ceux qui pensent avoir trouvé, avec l’exclusion de Pluton du cortège planétaire traditionnel, un nouvel argument contre l’astrologie !
Téléchargez-le dès maintenant dans notre
boutique