S’il vous est arrivé de lire une Histoire de l’astronomie revue et corrigée par un astronome contemporain vous comprendrez qu’il n’y a aucune tolérance à espérer des tentatives d’explicative de l’astrologie par l’astrométrie. Question de territoire : impossible de douter du dogme ; en cas d’erreur on verra plus tard. Ainsi l’histoire des sciences à usage scolaire est présentée comme une évolution sans bavures, de la nuit des origines à la lumière d’aujourd’hui. Revenir sur son passé serait pire que déboulonner Staline [2]. Savant, politique ou religieux, l’Homme — fonction solaire — a besoin d’Histoire sainte. Cette fonction l’entraîne à éliminer ou domestiquer les autres fonctions, nier les contradictions (Mars), farder les squelettes du placard (Pluton) afin de sortir toujours plus beau de son bourbier d’animal terrestre. Un philosophe des sciences, Karl Popper, bat le record du sophisme : il n’y a de vraie science que la science qui se trompe (faillible). Popper est du Lion (induction positive), j’ai déduit son Signe de son “plus je me trompe, plus j’ai raison” et je ne me suis pas trompé, donc l’astrologie n’est pas une science.
La constante de gravitation a-t-elle un caractère absolu ?
Mme Suzel Fuzeau-Bræsch a eu l’idée de soumettre Harmonie des pesanteurs à la critique d’un de ses amis, paraît-il astronome, probablement celui qui l’a conduit à écrire que le zodiaque tropique (je cite) : “… n’est, scientifiquement, qu’une méthode pratique permettant de repérer la position de la Terre sur son orbite autour du Soleil…” Une méthode pratique et pardon, scientifique, qui détermine les durées de jour et nuit, les variations annuelles d’ensoleillement Nord-Sud… voilà qui mérite un Prix (d’excellence) au concours Lépine. Qu’il s’agisse du même ou non, il fallait s’attendre à un massacre. Son auteur n’ayant pas daigné mentionner son identité, je l’appelle Mouchassieux.
Dès la première page il fustige d’un point d’exclamation ma réserve sur le caractère absolu de la constante de gravitation G [3]. Je présente son universalité de lieu et d’époque comme une hypothèse, ce qui irrite mon con-noteur : elle est prouvée ! note-t-il en marge et en rage. Réponse : voici ce qu’on peut lire, en 1999 dans le Traité de Physique d’Eugene Hecht (ouvrage destiné aux étudiants du 1er cycle en sciences et aux classes préparatoires aux écoles d’ingénieur) :
“La quantité G est une mesure de l’intensité de la force gravitationnelle. Étant un nombre extrêmement petit, FG n’est appréciable que lorsqu’au moins l’une des masses en interaction est très grande. Cependant, étant de portée infinie (elle tend vers zéro quand r proche infini), et étant toujours attractive (donc non-atténuée par de possibles forces répulsives), la gravité détermine les propriétés de l’Univers à grande échelle. Par conséquent, la gravité joue un rôle central dans les théories cosmologiques. Sur cette toile de fond sont récemment venues se plaquer d’intéressantes suggestions que G pourrait n’être pas une constante.”
J’ai mis en gras ce qui mouche Mouchassieux. Bien avant 1999, la discussion sur la variabilité de G était ouverte. Selon le physicien Paul Dirac (1902–1984), cette constante inconstante devait être inversement proportionnelle à l’âge de l’Univers et, par conséquent, diminuer avec le temps cosmique. L’hypothèse fut très controversée dès son énoncé en 1938. Des années plus tard, P. Dirac n’en démordait pas : G devait varier. L’ouvrage de Georges Gamow, La Gravitation [4], fait état de la controverse au chapitre des Problèmes non résolus. En 2001, le dossier n’est pas fermé, en 1982, pour un Mouchassieux, il n’a jamais existé !
Page suivante (109) j’ai écrit, je crois que je peux encore le faire : “peu de gens savent que leur poids est une force en relation avec leur masse et la valeur du champ de pesanteur au lieu qu’ils occupent.” Mouchassieux souligne “poids” et commente : “tous les lecteurs de Tintin le savent.” Après ce trait d’humour, on ne peut plus douter du comique de la suite : un débit d’insultes avec des formules, reprises dans l’article, et des gribouillis s’appliquant à démontrer que les périodes calculées par les demi-grands axes planétaires et les gravités moyennes n’ont pas lieu d’exister…

Pour comprendre Newton lisez Hergé mais pour Spinoza rien ne vaut Édika (Album 22).
L’article expose des résultats cohérents et chiffrés de relations entre les données orbitales (L), les masses (m) et les rayons (r) moyens des planètes. Ces variables naturellement sans lien entre elles, apparaissent liées dans le système solaire pour les planètes principales, et c’est la formule du pendule qui fait apparaître ce lien par un ensemble conforme à un modèle astrologique, non-conforme aux paradigmes des physiciens… anti-astrologues. En conséquence, Mouchassieux ne s’attaque pas aux résultats chiffrés. Ils ne l’intéressent pas plus que l’hypothèse de Dirac ; ils sont éjectés avant d’être lus parce que les variables citées doivent rester indépendantes. Un bilan qui donnerait une idée contraire (rejoignant l’astrologie et, nous verrons plus loin d’autres recherches) est impensable par principe. Notre pitbull du temple scientiste, pas fou, nie les relations en proposant de ne pas prendre le rayon de la planète là où il est pour donner g (intensité moyenne de la gravité à la surface) : “Pourquoi prendre g à la surface de la Terre, écrit-il, et non à la surface de la lune, ou à celle d’un satellite artificiel ?” Réponse : parce que le rayon de la Terre n’est pas égal à la distance Terre-Lune. En prenant g à n’importe quelle distance du centre d’une planète, comment pourrait-on supposer une relation entre le demi-grand axe et le rayon puisque celui-ci n’est pas pris en compte ? Mme Suzel Fuzeau-Bræsch, spécialiste des statistiques, devrait calculer la probabilité, en combinant L, m, r, de trouver des symétries organisées selon un modèle rationnel préalablement défini. “Je fais n’importe quoi, écrit le Mouchassieux, jusqu’à ce qu’il y ait quelque chose qui marche.”
Le “n’importe quoi” est la formule du pendule simple
Une formule qui dans l’histoire des sciences n’a pas intrigué n’importe qui. Mais, comme l’écrit Mouchassieux en conclusion (ce sera ma dernière citation) : “Rien d’harmonieux… de la pata-astronomie par un esprit faux et confus. Que ne peut-on pas faire en manipulant nombres et formules ? L’état d’esprit de l’auteur doit être voisin de celui qui régnait au XVIe siècle, mais il ne se justifie plus, pas plus que l’astrologie d’ailleurs.”
J’ai souligné l’aveu du préjugé radical d’un grotesque (insulte galiléenne) de ce siècle, et en tant que réincarné de la Renaissance retournant à mon époque par mes documents de bibliothèque, j’ai retrouvé un petit ouvrage sur La Terre et le pendule [5] où l’idée d’associer le pendule aux mouvements célestes apparaît chez un esprit fumeux : Galilée. Aujourd’hui, jugée comme un erreur (et pourtant, il oscille) elle ne figure pas dans l’histoire officielle du Héros, ni dans les albums de Tintin :
Galilée formula la loi de l’inertie et étudia la chute libre des corps. Il essaya même, bien que sans succès, d’appliquer la mécanique terrestre à l’explication des mouvements des corps célestes. Ainsi, par exemple, comparaît-il la Terre et la Lune à deux poids fixés à la tige d’un pendule attachés au Soleil.
Puisque la Lune tourne autour de la Terre, disait-il, sa distance, par rapport au Soleil, est variable. Ce pendule gigantesque est donc tantôt plus court, tantôt plus long.
La suggestion d’un lien tendu entre notre planète et le Soleil par un fil imaginaire tel celui d’un pendule n’est pas nouvelle. Le fondateur de la physique moderne s’en est rendu coupable. En logique mouchassienne, il doit être comme moi, pata-astronome.
Mais à la différence de Galilée, je ne prends pas le corps céleste comme une énorme boule oscillante, j’imagine l’oscillateur, sans précision de matière et de dimension, à la surface de l’astre. Là encore, un esprit confus y a pensé avant moi mais après Galilée :
Nous avons déjà vu combien le pendule est sensible aux moindres variations de la pesanteur terrestre…
Mais le pendule n’est pas seulement un appareil “terrestre”. Il est aussi influencé par l’attraction de la Lune et par celle du Soleil.
Dès le XVIIe siècle, Lomonossov [6] indiquait la possibilité de percevoir des “forces cosmiques” sur la surface terrestre à l’aide du pendule. (La Terre et le Pendule).
Un objet matériel oscillant réagit aux moindres variations de la pesanteur terrestre, que dire d’un objet vivant composé d’oscillateurs internes organisés, plus nombreux et plus sensibles ? F. Boubléinikov poursuit :
Si l’on pouvait avoir un pendule de 120 km de long, il s’écarterait sous l’influence de l’attraction lunaire de presque d’un centimètre de la direction qu’il prend normalement sous l’action de la pesanteur terrestre, et changerait de position suivant le déplacement de la Lune dans le ciel.
Mais les pendules dont les savants peuvent disposer sont mille fois plus courts. Leur longueur ne se mesure qu’en mètres. Et les écarts réels qu’ils permettent de déterminer sont également des milliers de fois plus petits.
La mathématique mesure le réel et le dépasse par des expériences mentales irréalisables, des équations purement spéculatives. Le pendule de 28 kg de Jean-Bernard Leon Foucault (1819–1868) conçu pour prouver (1851) la réalité de la rotation de la Terre autour de son axe, n’avait que 67 m (ou 60 m) de long. Pourquoi pas 200, 300, 1000 mètres… pourrait-on demander à Mouchassieux ? Quelle loi mathématique, à part les limites des moyens techniques, interdit de concevoir un pendule d’une longueur au-delà de la Terre, quelle règle impose des interdits aux développements spéculatifs d’une formule mathématique ? Galilée, Lomonossov n’ont pas craint une extrapolation qui n’a de défaut que lorsqu’un astrologue en use.
Parfaitement conscient du caractère singulier de résultats épouvantables pour les astronomes, j’ai exprimé mes réserves, non pas sur les chiffres, mais sur leur interprétation physique. La formule du pendule n’est peut-être qu’une piste qui conduit à autre chose.
Trois directions d’interprétation physique
Jusqu’ici je n’ai supposé que trois directions d’interprétation physique :
a) — Hypothèse osée : les résultats sont conformes à un état originel du système solaire.
b) — Hypothèse positiviste : Aucune référence à un originel. Les résultats ne sont pas à interpréter. Ils expriment un état sous-jacent à l’état réel.
c) — Hypothèse combinée : a) est devenu b) en laissant des traces. Un paramètre supplémentaire, une lecture différente de la formule du pendule rendent compte d’un aspect inconnu du système solaire contemporain.
L’article des Cahiers no 5 ne traite que de l’hypothèse a) en imaginant un système planétaire aux distances moyennes d déduites des périodes T par la 3e loi de Kepler : le cube de la distance = le carré de la période (D3 / T2 = 1) sans coefficient de proportionnalité [7]. Cette hypothèse, qui n’a rien d’une certitude, m’a permis de montrer les relations entre les valeurs obtenues et de les transformer selon les règles mathématiques pour poser l’équation la plus simple. Un exercice qui n’a pas dérangé d’un iota le système solaire actuel mais qui a ouvert des horizons. Ceux qui me tiennent toujours à cœur demandent à sonder dans les cycles biologiques lesquels correspondent aux périodes du rapport √(L / g). Un moyen de vérifier si ces périodes ou leurs harmoniques (au sens mathématique et non pas mystique comme Mouchassieux a voulu l’entendre) existent concrètement. À mon appel d’informations personne n’a répondu, surtout pas les “associations de recherches sur les rythmes astrologiques” [8] qui jouent la carte du “grand R” en rivalisant dans le “non-E”.
J’ai abordé dans l’article de janvier 82 l’hypothèse b) par ces lignes que Mouchassieux n’a pas soulignées :
Ceux qui n’osent imaginer une oscillation de période Tg inconnue des astronomes, non mesurée et peut-être absurde, ont la ressource de se dire qu’il s’agit d’une sorte de coefficient planétaire, tel que [9] :

Chaque identité planétaire se trouve ainsi définie par sa période T de révolution sidérale et par le rapport que donne le champ de gravitation f3 dans lequel elle se trouve avec le champ g qu’elle crée elle-même à sa surface.
L’hypothèse c) m’a parue admissible après lecture d’un article de D. Lesueur (Ciel et Espace no 173) sur les étoiles variables périodiques : les Céphéides [10]. Leurs périodes sont de l’ordre des résultats trouvés (d’un jour à quelques semaines) et l’alternance de dilatation-contraction du rayon a été comparée à l’oscillation d’un pendule. Comparaison qui vaut plus qu’une analogie puisque les auteurs d’un ouvrage d’astronomie en donnent la formule en s’étonnant de sa parenté avec celle du pendule. Que ne consultent-ils Mouchassieux pour sortir d’une méprisable Renaissance !
Dans le cas le plus simple des pulsations d’une sphère homogène la période des oscillations Π3 est liée à la densité moyenne de la sphère ρ3 par la relation :

(où ρ3 est en kg ⋅ m−3 et γ est le rapport des chaleurs spécifiques pour le matériau stellaire, soit 5/3 pour un gaz monoatomique.)
Il est curieux que cette expression se déduit de la formule connue des oscillations d’un pendule, si au lieu de la longueur l’on y porte le rayon de l’étoile et si on tient compte de l’accélération de la pesanteur à la surface de l’étoile :

(Astronomie. M. Dragrev, V. Demine, I. Klichine, V. Tcharouguine. Éditions MIR. Moscou. 1983).
Ce que j’ai mis en gras coiffe Mouchassieux d’un bonnet d’âne : pour calculer la période d’une étoile Céphéide on prend la gravité à la surface et non sur un satellite. Ceci dit, contrairement à sa critique, le Soleil étant une étoile, je l’ai placée au centre d’une sphère de rayon moyen 5,32 UA [11] voisine de l’orbite de Jupiter avec, pour la contraction, les demi-grands axes inférieurs à cette distance (orbites des astéroïdes à Mercure), et pour la dilatation les demi-grands axes supérieurs (Saturne à Pluton).
Le rayon de l’étoile Soleil étant Lp (demi-grand axe de la planète p), j’ai pris comme accélération à la surface, non pas la force centrale [12] :

mais celle de la planète à la surface :

Imaginons une grande sphère de rayon 4,96 UA (périhélie de Jupiter) en contact à une plus petite de rayon 11,2 fois plus grand que celui de la Terre, de masse 318 fois plus grande, et qui communique son intensité de gravitation à la surface au cercle de 4,96 UA, vous aurez une représentation schématique de mon hérésie : j’ai géométrisé le contact d’un grand cercle (celui de la sphère solaire) et d’un plus petit (celui de la planète) en supposant que l’intensité g de la planète (ou sa densité) pouvait s’expliquer par une relation, un lien entre L (demi-grand axe), m (masse de la planète), M3 (masse du Soleil), r (rayon de la planète).
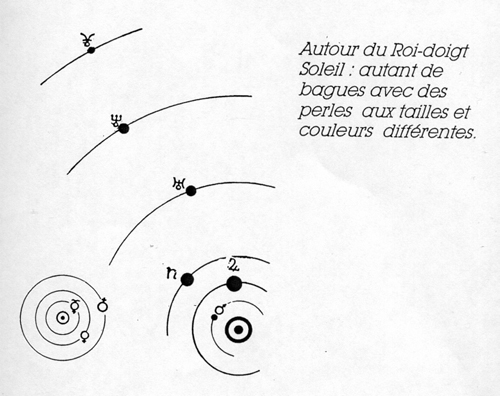
Porte ouverte à un balourd, cette céphéide est originelle ou potentielle. Je n’ai jamais dit qu’elle existait autrement que par les formules citées. Et, selon un souci de visualisation qui sacrifie l’abstraction mathématique à l’intuition concrète, pour montrer, dans la formation des planètes du système solaire les relations entre les variables (en soi indépendantes) de L, r, m, j’ai pris l’image d’un anneau (L) portant une perle (la planète) de masse m et de rayon r, les indépendantes devenant liées par la force centrale.
En abandonnant les forces newtoniennes pour la géométrie relativiste de l’espace-temps, le rapport f3 / g suggère l’interférence d’une courbure sur une autre : celle d’une balle prise dans un cerceau, d’une perle soudée à un anneau. Dans la Cosmogonie Astrologique j’ai comparé l’orbite à la bague, la planète à la perle, pour avancer l’idée que les deux, la distance au Soleil et le rayon de l’astre, ne sont pas indépendants. À la surface de la Terre, nous sommes entre deux courbures ou pris par les deux et davantage.
L’idée de lier l’anneau orbital au rayon de l’astre n’est pas nouvelle. Lothar Komp, auteur d’un article original sur l’Harmonie du système planétaire (Fusion no 69 — janvier 1998) rappelle que J. Kepler y avait pensé :
“Si l’on met en rapport les périodes des planètes avec leurs diamètres, on constate, comme le suspectait Kepler, que l’accroissement de la taille des planètes est proportionnel à celui de leur période.” (Cahiers conditionalistes no 27 — 1998).
Proportionnel est un peu fort, et la relation entre L (déduit de la période) et r est meilleure si l’on prend r2 au lieu de r et si l’on tient compte de la masse m : une perle avec ses dimensions de rayon et densité.
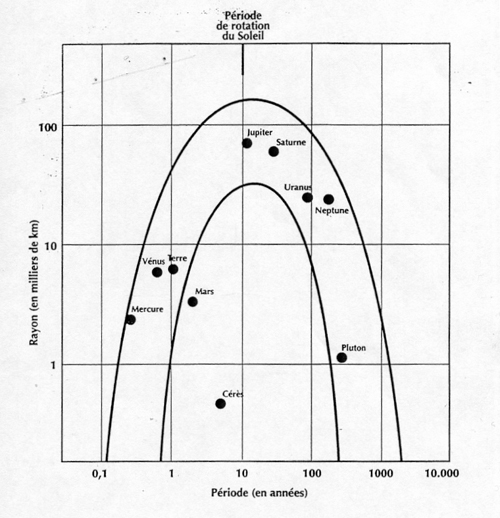
Les planètes du système solaire - Figure 3 de l’article de Lothar Komp (Fusion no 69) : Si l’on met en rapport les périodes des planètes avec leurs diamètres, on constate, comme le suspectait Kepler, que l’accroissement de la taille des planètes est proportionnel à celui de leur période.
Après l’anneau et sa perle, en décomposant la formule du pendule j’ai pensé au volume d’un tore.
a) Formule du pendule :

b) g moyen étant égal à la constante gravitationnelle de la planète (G que multiplie la masse m de la planète) divisée par le rayon moyen (r) élevé au carré (r2), la formule ci-dessus s’écrit également :

c) le volume d’un tore de section r, de circonférence 2 π L est égal à :

r est égal au rayon moyen de la planète. L à son demi-grand axe. L’espace-temps d’une planète n’est plus une “rigole” (voir ouvrages de vulgarisation de Tintin et Milou) mais un tore.
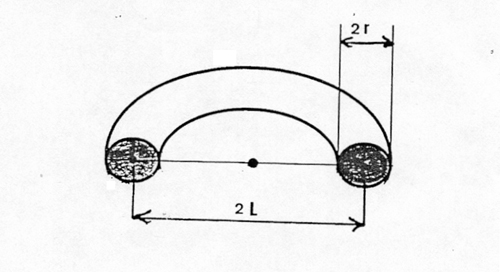
d) La masse volumique étant égale au quotient masse/volume, en divisant la masse de la planète m par le volume déterminé par son demi-grand axe (L) et son rayon au carré (r × r), on obtient la masse volumique du tore théorique ou originel qui aurait la masse de la planète.

e) L’opération d) revient à multiplier 1 / Tg2 (fréquence au carré) de la formule b) par 2 / G.
Cette dernière remarque pourrait accréditer l’hypothèse Dirac d’une variation de G avec le temps. Autre information encourageante venue d’une lecture en début d’année : le temps est cosmologiquement lié à la densité :
“Il faut de plus en plus de temps pour que l’aspect à grande échelle de l’univers soit modifié de manière sensible. Il en résulte que plus on s’approche de t = 0 (commencement de l’univers) plus court est le temps nécessaire au développement de changements significatifs. Le temps caractéristique est grossièrement proportionnel à l’inverse de la racine carrée de la densité de l’univers à n’importe quelle époque (plus la densité est importante, plus court est le temps caractéristique), et au début de l’ère dominée par les photons, les électrons, les positons et les neutrinos, cette échelle de temps ne valait que 0,02 seconde.” (John Gribbin, À la poursuite du Big Bang, Champs Flammarion.)
Pas d’hérésie : la période T est bien proportionnelle à l’inverse de la racine carrée de la masse volumique dans la formule des étoiles céphéides comme dans l’opération d).

alors :

En février dernier, après avoir lu Gribbin j’en étais là et las de mes réflexions, lorsqu’un nouvel article de Fusion, Un modèle magnétohydrodynamique de formation planétaire [13] a apporté aux équations citées l’expérience qui leur manquait : la matière d’un tore peut devenir un anneau, puis une planète.
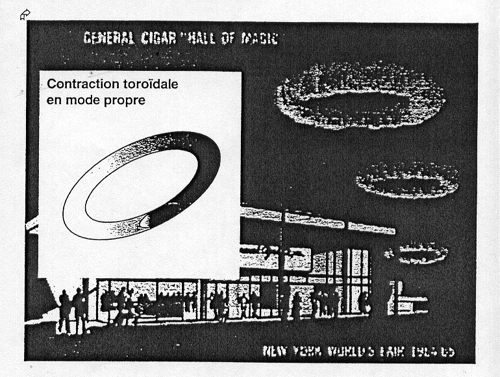
D. Wells, désigne par effet “White Owl” la condensation de matière d’un anneau en une boule au sein de cet anneau.
La matière d’un tore peut devenir un anneau, puis une planète
En 1960, le Pr Bob Mark, un collègue ingénieur à Princeton, a été embauché par la General Cigare Company, fabricant du cigare White Owl, pour concevoir une machine qui réaliserait des anneaux de fumée de 3 mètres. Mark est très doué et il y parvint. C’était sa machine qui réalisa les magnifiques ronds de fumée de l’Exposition internationale de New York en 1964–1965… Surprise des spectateurs, les ronds de fumée se mettent en boule ! Ces anneaux montaient à une hauteur d’environ 12 à 15 mètres, puis s’arrêtaient. Vous pourriez penser qu’ils resteraient suspendus pendant un certain temps puis se disperseraient progressivement, mais ce n’était pas le cas. Les anneaux s’élevaient, s’arrêtaient pendant un certain temps et, soudainement, la fumée se déplaçait azimutalement autour de l’anneau pour produire ce qui ressemblait à un coup de tonnerre. Soudainement, au lieu d’un anneau, il y avait une boule de fumée. Transposons maintenant cela au cas de la formation des planètes : imaginez que ce cylindre — le gâteau roulé de plasma — se forme dans le plan de la galaxie, et est raccourci en disque. C’est alors que se produit l’effet White Owl. Maintenant au lieu de l’anneau cylindrique, nous avons une structure en forme de boulet de canon de gaz se déplaçant autour de l’orbite qui était décrite par l’anneau. Elle se déplace avec la même vitesse azimutale que celle de l’anneau car le moment angulaire est conservé.
Les italiques sont de l’auteur. Le reste de l’article ne présente rien de commun avec les Éléments de Cosmogonie. Daniel Wells justifie la loi de Titius-Bode qui est imprécise et linéaire, alors que les rapports des demi-grands axes renvoient aux formules des raies spectrales et à des moments angulaires couplés. Le scénario de D. Wells transforme le tore en anneau, l’anneau en planète, alors que je n’exclus pas les enveloppes sphériques d’une céphéide avant les “cylindres de plasma”. L’idée de transformation du tore en anneau n’est pas originale. Celle du tore en boule m’était inconnue, sa démonstration expérimentale la rend incontournable.
Figure 5 de l’article de Daniel Wells
L’effet “White Owl”. Bob Mark a construit une machine capable de produire des ronds de fumée magnifiques de 3 mètres. Cette machine fut présentée au pavillon de la General Cigar Company à l’Exposition Internationale de 1965. Au moment où l’auteur observait le comportement des ronds de fumée, il découvrit quelque chose d’étonnant : plutôt que de se disperser normalement, la fumée ou le gaz formant chacun des anneaux stables se condensait soudainement pour produire une boule au sein de l’anneau (Fusion no 86)
La voie que j’ai suivie est à la fois plus simple, plus précise et plus ardue.
▶ Simple : les rapports de distances, la formule du pendule, sont des formules élémentaires.
▶ Précise : les résultats, pour les demi-grands axes sont inférieurs à une incertitude de 0,08 %. Ceux, inédits, du rapport L̄ / ḡ à une incertitude moyenne de 2 %.
▶ Ardue : elle met en cause l’interaction gravité-électro-magnétisme, et je n’ai pas la prétention d’avoir résolu un problème qui reste un casse-tête pour les physiciens.
| Tableau des données |
| Planètes |
Demi-grand
axe L̄ (UA) |
Masse m̄
(l = 1) |
Rayon r̄
(l = 1) |
| Soleil |
5,32 |
332 948 |
109,25 |
| Mercure |
0,387 |
0,055 |
0,383 |
| Vénus |
0,723 |
0,814 |
0,95 |
| Terre |
1 |
1 |
1 |
| Mars |
1,524 |
0,107 |
0,53 |
| Jupiter |
5,202 |
318 |
10,97 |
| Saturne |
9,55 |
95,2 |
9,14 |
| Uranus |
19,22 |
14,54 |
3,98 |
| Neptune |
30,11 |
17,15 |
3,87 |
| Pluton |
39,44 |
0,002 |
0,19 |
Avec en unités terrestres :
- L̄ = L / Ll, où Ll = unité astronomique (UA) = 1,495 978 7 × 1011 m
- m̄ = m / ml, où ml = masse Terre = 5,9736 × 1024 kg.
- r̄ = r / rl, où rl = rayon moyen Terre = 6 371 km.
| Tableau des résultats |
| Planètes |
ḡ / L̄ =
m̄ / (L̄ ⋅ r̄2)
(l = 1) |
m / (2π2 ⋅ L ⋅ r2)
= ρtore
(kg ⋅ m−3) |
g / L
= ω2 (rad2⋅ s−2) |
g / (4π2 ⋅ L)
= 1 / Tg2
(s−2) |
Période
Tg
(jours) |
∛(ḡ / L̄)
= ∛A
(l = 1) |
| Soleil |
5,244 |
0,261 |
3,44 × 10−10 |
8,72 × 10−12 |
3,92 |
1,737 |
| Vénus |
1,247 |
0,0622 |
8,20 × 10−11 |
2,08 × 10−12 |
8,03 |
1,076 |
| Mercure |
0,974 |
0,0485 |
6,39 × 10−11 |
1,62 × 10−12 |
9,10 |
0,991 |
| Terre |
1 |
0,0498 |
6,56 × 10−11 |
1,66 × 10−12 |
8,98 |
1 |
| Jupiter |
0,507 |
0,0253 |
3,33 × 10−11 |
8,43 × 10−13 |
12,6 |
0,798 |
| Mars |
0,249 |
0,0124 |
1,64 × 10−11 |
4,14 × 10−13 |
18,0 |
0,629 |
| Saturne |
0,119 |
5,93 × 10−3 |
7,81 × 10−12 |
1,98 × 10−13 |
26,0 |
0,492 |
| Uranus |
0,048 |
2,38 × 10−3 |
3,14 × 10−12 |
7,96 × 10−14 |
41,0 |
0,363 |
| Neptune |
0,038 |
1,90 × 10−3 |
2,50 × 10−12 |
6,33 × 10−14 |
46,0 |
0,337 |
| Pluton |
1,49 × 10−3 |
7,97 × 10−5 |
1,05 × 10−13 |
2,66 × 10−15 |
224 |
0,114 |
|
A |
B |
C |
D |
E |
F |
Avec en unités terrestres :

et en unités SI :

Aussi, plutôt qu’un scénario approximatif, je livre les relations chiffrées entre L, m, r, qui reproduisent les symétries du R.E.T. et autorisent, étant donné leur ordre de précision, à traiter les mouchassieux de mouches inertielles, ou mouches à M ⋅ R2 [14].
Les résultats des colonnes A et F sont en unités terrestres. On transforme en unités SI (mètre, kilogramme, seconde) en multipliant les résultats de la colonne A par : 0,9835. Coïncidence due aux unités choisies, pour la Terre l’ordre de grandeur du produit L ⋅ r2 est celui de la masse (1024). Les résultats de F se multiplient par ∛(6,5645 × 10−11) soit environ 4,034 × 10−4 pour donner les ∛(g / L) physiques.
Une seule colonne suffirait, étant toutes liées par des coefficients de proportionnalité. Les racines cubiques de la colonne F ∛(ḡ / L̄) en unités Terre, s’expriment, avec une marge d’incertitude inférieure à 2 % (moyenne), par la formule :
- De Soleil à Mars : 0,632 + 1,321 × u / (1 − u)
- De Mars à Pluton : 0,632 − 1,321 × u / (1 + u)
Les valeurs de u sont :
- 0,361 pour Soleil et Pluton.
- 0,180 pour Vénus et Neptune
- 0,159 pour Mercure et Uranus
- 0,078 pour Jupiter et Saturne
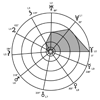
Les deux formules se réunissent dans une seule figure probablement plus compréhensible que son expression algébrique :
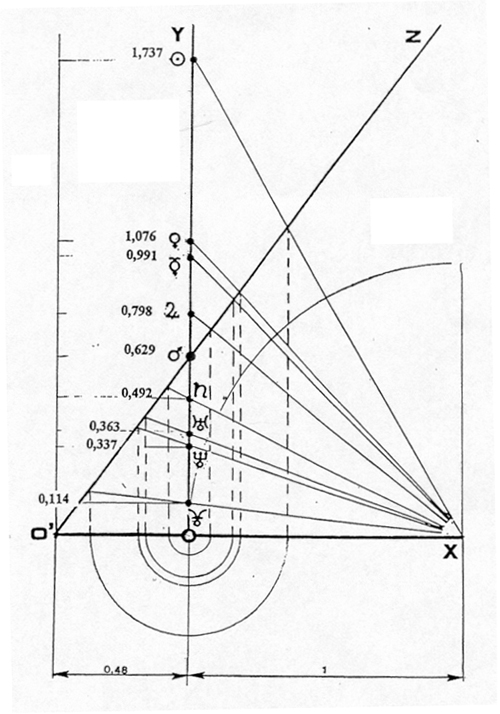
Les valeurs portées en Y sont les valeurs réelles.
On détermine les valeurs sur l’axe des X (abscisse) par 0,48 ± u (rayons successifs des cercles concentriques : 0,361 ; 0,180 ; 0,159 ; 0,078 ; 0). Le résultat est multiplié par le coefficient (tangente) de la pente O′Z = 1,321, et le produit obtenu se divise par 1 ± u. Ex : Soleil, u = 0,36.
- 0,48 + 0,36 = 0,84
- 0,84 × 1,321 = 1,109
- 1,109 / (1 − 0,36) = 1,732
Les signes ‘+ −’ sont inversés pour le symétrique, Pluton.
Une formule peut s’exprimer de différentes façons pour un résultat identique. Ainsi, en partant de ‘0’ sur l’abscisse les formules précédentes s’écrivent :
- Soleil à Mars : 1,321 × (0,48 + u) / (1 − u) = ∛(ḡ / L̄)
- Mars à Pluton : 1,321 × (0,48 − u) / (1 + u) = ∛(ḡ / L̄)
Pour avoir 0,632 et les mêmes résultats que par les formules précédentes, on prend 0,478 au lieu de 0,48 qui est une valeur arrondie. Avec 0,632 les formules donnent :
| Planètes |
u |
∛(ḡ / L̄) réel |
∛(ḡ / L̄) calculé |
ḡ moyen
= m̄ / r̄2 |
ḡ calculé |
Écart sur r (%) |
| Soleil |
+0,361 |
1,737 |
1,735 |
27,9 |
27,4 |
+0,9 |
| Vénus |
+0,180 |
1,076 |
1,058 |
0,9 |
0,86 |
+2,2 |
| Mercure |
+0,159 |
0,991 |
0,998 |
0,38 |
0,39 |
−1,3 |
| Terre |
+0,159 |
1 |
0,998 |
1 |
1 |
|
| Jupiter |
+0,078 |
0,798 |
0,797 |
2,64 |
2,64 |
|
| Mars |
0 |
0,629 |
0,632 |
0,38 |
0,39 |
−1,3 |
| Saturne |
−0,078 |
0,492 |
0,491 |
1,14 |
1,13 |
+0,4 |
| Uranus |
−0,159 |
0,363 |
0,364 |
0,92 |
0,93 |
−0,5 |
| Neptune |
−0,180 |
0,337 |
0,336 |
1,15 |
1,14 |
+0,4 |
| Pluton |
−0,361 |
0,114 |
0,114 |
0,059 |
0,058 |
|
|
A |
B |
C |
D |
E |
F |
Avec :
- D : Revient à élever au cube les valeurs de B et à multiplier par le demi-grand axe L̄.
- E : Même calcul : ḡ (moyen calculé) = valeurs de C au cube × L̄.
- F : ḡ s’obtient par m̄ / r̄2. Le calcul du % d’écart doit donc être la racine des rapports ḡ observé (D) et ḡ calculé (E).
Les valeurs moyennes de ḡ sont obtenues par des données pures de masse et rayon, il n’est pas tenu compte de la vitesse rotation de l’astre, des variations de ḡ moyen selon les latitudes, etc. Ces paramètres ne modifieront guère les valeurs ci-dessus. L’ordre de précision de ± 1,5 % est largement satisfaisant… ou inquiétant pour les mouches inertielles qui ne verront dans ce tableau, conforme à un modèle astrologique, qu’une conjuration de coïncidences ; car c’est ainsi qu’on “raisonne” dans la pseudo-science anti-astrologique.
La Terre dépare dans ce tableau, ou alors nous sommes en plein géocentrisme objectif, le R.E.T. n’existant que par rapport à une position terrestre qui paraît subjective mais peut-être objectivement particulière. Perfide, j’ai caché la Lune pour laisser un dernier espoir au symbolisme anti-signal. La voici, elle rétablit l’ordre astrologique que la Terre semble perturber. En supplément, deux astéroïdes principaux pour tester nos formules : Cérès et Vesta.
| Données complémentaires |
| Astres |
Demi-grand
axe L̄ (UA) |
Masse m̄
(l = 1) |
Rayon r̄
(l = 1) |
| Lune |
1 / 389 |
0,0123 |
0,273 |
| Cérès |
2,77 |
2 × 10−4 |
0,078 |
| Vesta |
2,15 |
4 × 10−5 |
0,044 |
| Résultats du calcul de u |
| Astres |
ḡ / L̄ =
m̄ / (L̄ ⋅ r̄2) |
∛(ḡ / L̄)
= ∛A |
ḡ moyen
= m̄ / r̄2 |
u |
| Lune |
65,64 |
4,034 |
0,165 |
+0,635 |
| Cérès |
0,0119 |
0,228 |
0,033 |
−0,260 |
| Vesta |
0,0096 |
0,213 |
0,021 |
−0,272 |
|
A |
B |
C |
D |
Les valeurs u se calculent par : (B − 0,632) / (B + 1,321)
ou rayon u = (∛ḡ − 0,632 × ∛L̄) / (∛ḡ + 1,321 × ∛L̄).
Le rayon u restituant ḡ ou ∛(ḡ / L̄) pour la Lune est donc sensiblement égal au coefficient qui donne Mars pour u = 0 et s’applique à toutes les planètes. Nous avons, en effet :
0,632 + (1,321 × 0,635) / (1 − 0,635) = 4,029
… au lieu de 4,034 (valeur moyenne, colonne B, de ∛(ḡ / L̄) pour Lune). Avec 4,029 le calcul de ḡ donne : 0,168. Écart de +1,8 % par rapport aux données m̄ / r̄2.
Cérès (0,228) est le double de Pluton (0,114). Une redondance. Lorsqu’on lit les textes inspirés de la mythologie sur les effets supposés de cet astéroïde, on baigne aussitôt dans les mystères des maîtres de la Nuit. Les symbolistes suivent malgré eux la logique du R.E.T. en attribuant la transcendance aux signaux faibles, et la multiplicité associée à ce niveau porte à prêter plusieurs visages à une seule fonction. Celle du Soleil n’a pas de doublures.
L’indice m̄ / (L̄ ⋅ r̄2) ou ḡ / L̄, pourrait se comprendre comme un moyen de classer qualitativement les signaux L, m, r. En haut de l’échelle, vers le Soleil : le proche, les rapports élevés entre les masses et les rayons. En bas de l’échelle, vers Pluton : le lointain, les rapports faibles entre masses et rayons. Au centre, autour de Mars, les valeurs moyennes. Mais la singularité quantitative des indices est dans la symétrie des échelons ou cercles de rayons u calculés avec les formules en bas de page 228 :
| Lune |
+0,635 |
|
| Soleil |
+0,362 |
Pluton |
−0,361 |
| Vénus |
+0,185 |
Neptune |
−0,178 |
| Mercure |
+0,155 |
Uranus |
−0,160 |
| Jupiter |
+0,078 |
Saturne |
−0,077 |
| Mars |
+0,0015 |
|
Le + ou − différencie les valeurs ∛(ḡ / L̄) supérieures (+) à 0,632 ou inférieures (−) à la cote de Mars. Ce dernier tableau ouvre des perspectives d’harmonisation : on prend les moyennes et une formule de rapports. Ainsi :
| Soleil - Pluton |
|
0,361 |
| Vénus - Neptune |
0,361 / 2 = |
0,1805 |
| Mercure - Uranus |
|
0,1578 |
| Jupiter - Saturne |
0,1578 / 2 = |
0,0789 |
Et : 0,0789 × 0,361 = 0,1578 × 0,1805 = 0,0285 (arrondi)
Ces relations relèvent de l’esthétique, les données moyennes et l’incertitude sur ḡ ne permettent pas d’affirmer mais de suggérer des relations possibles entre les valeurs expérimentales. On parle alors de modèle plus ou moins satisfaisant. Celui-ci ne s’éloigne guère des % d’écart déjà calculés (tableau page 227). Les % satisfaisants sans modèle suffiraient à valider les résultats, mais l’esthétique a ses droits. Celle des symétries appelle des investigations inédites sur les objets du système solaire. Pour les orbites principales nous avons nos + et − conformes aux symétries du R.E.T. Qu’en est-il des astéroïdes et satellites ? Pour la Lune en inversant le signe ‘+’ de son rayon u on trouve sa symétrie à −0,126, du côté de Pluton et des “petits corps”. L’inversion de signe pour Cérès donne un résultat inattendu : 1,318… valeur proche du coefficient 1,321 obtenu par une formule de corrélation linéaire entre les ∛(ḡ / L̄) de Mars à Soleil et les ∛(ḡ / L̄) de Mars à Pluton.
Après cette mise à jour, les développements peuvent se compléter dans les directions géométriques, astrophysiques, esthétiques spéculatives.
a) géométriques : l’analyse formelle des propriétés des différentes figures (puissance des points, faisceau de droites, angles, tangentes, pour la figure page 226) peut inspirer des hypothèses explicatives.
b) astrophysiques : elles demanderont le concours de spécialistes mieux embouchés que des Mouchassieux et capables d’imagination extra-scolaire. Ou bien, les experts nous aideront à leur insu par leurs articles, comme ceux de Fusion qui se soucient peu des recherches astrologiques mais nous valent d’avoir progressé.
c) esthétiques : elles rejoignent les géométriques et les physiciennes par des a priori platoniciens sur l’ordonnancement du système solaire ou du monde, tel celui des symétries ou des rapports harmoniques au sens mathématique, mais aussi musical à l’entendement.
Ellipses cosmologiques
La dernière figure se classe en a) et b). Avec les valeurs pures des rayons u on construit une ellipse qui évoque un mandala. Bien malin celui qui pressentirait la présence des rapports g / L du système solaire et de la Lune dans celui-ci. Les symboles vivants (ceux qui ont échappé aux momifications livresques) nous cachent les signaux. L’inverse est possible : à partir de données objectives, voilà une ellipse qui a une allure de Temple avec une porte fermée sur ses secrets et sur laquelle j’écrirais :
Interdit aux touristes, aux zozotéristes et aux mouches à M ⋅ R2
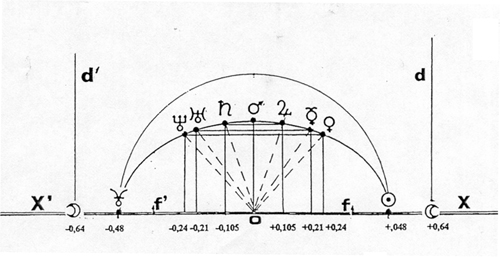
Ellipse cosmologique
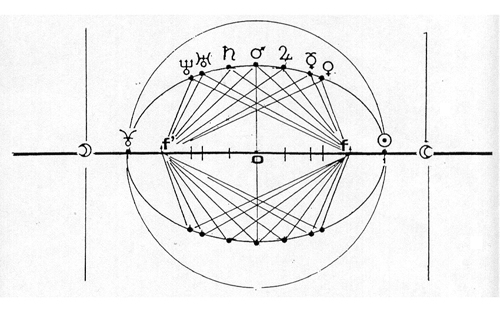
| Demi-grand axe |
a |
0,48 |
| Demi-petit axe |
b |
0,317 |
| Distance focale |
c |
0,36 |
| Excentricité |
e = c / a |
0,75 |
| Directrice |
a2 / c |
0,64 |
| Paramètre |
b2 / a |
0,21 |
Somme des vecteurs : ν + ν′ = cte = 2 ⋅ a. Les vecteurs, à partir de f′ sont égaux à : ν = 0,48 + u. On obtient ∛(ḡ / L̄) par : ∛(ḡ / L̄) ≈ 1,321 × ν / (1,43 − ν)
ou ± x = e ⋅ u soit 0,75 × (± u) par : 1,321 × (0,64 ± x) / (1,33 ± x)
On multiplie par 6,5645 × 10−11 pour avoir la pulsation ωg en unités SI.
L’ellipse ne se limite pas à la trace d’une orbite dans l’espace-temps. On retrouve des courbes elliptiques et hyperboliques dans les images d’interférences crées par deux sources de radiations (deux foyers) de même longueur d’onde et dans les résultantes ou compositions de deux vibrations perpendiculaires. L’ellipse qui se déduit des formules et de la figure (page 226) illustre les symétries et suggère par sa géométrie une formation des planètes combinant interférences et directions privilégiées. Dans les Éléments de Cosmogonie j’ai associé ces directions aux rayonnements de l’atome d’hydrogène pour certaines transitions. Ce n’est pas une hérésie : les masses planétaires ou la fumée des anneaux de la machine de Bob Mark ne doivent pas se concentrer n’importe où.
Un Mouchassieux rétorquera qu’il est inacceptable de lier des dimensions physiques à des rapports trigonométriques obtenus par des longueurs. À cela, en attendant de traiter cette question à fond, on peut répondre que les demi-grands axes ne sont pas des longueurs ordinaires, des distances comparables à Paris-Marseille ou Moscou-Tamanrasset (politiquement mesurée par Ch. De Gaulle). C’est une grave erreur de la physique classique que d’avoir confondu longueur et distance. Les angles de la figure 1 s’obtiennent aussi bien par les demi-grands axes assimilés (par image simplifiante) à des longueurs que par les rapports des vitesses moyennes élevées au carré correspondant à ces distances. Il va de soi que la distance Paris-Nice de 1000 km ne donne pas la vitesse moyenne des véhicules en circulation dans cette ville, parce que Nice ne gravite pas autour de Paris, pas plus que Tamanrasset autour de Moscou. Les anti-astrologues qui jouent sur les grandes distances des planètes pour ridiculiser l’astrologie sont des Mouchassieux ignares, à moins qu’ils ne soient surconscients dans leur passion de phobiques.
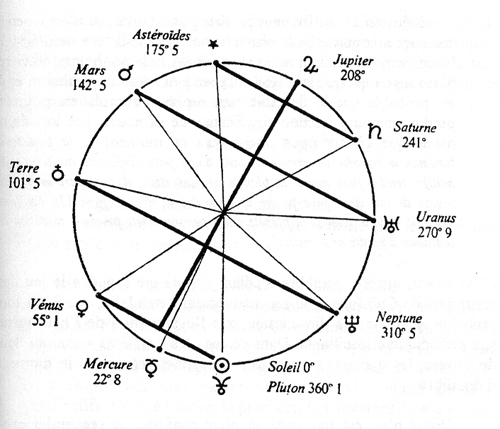
Gravitation et électromagnétisme
Il y a mieux que l’argument des distances. Le triangle formé de deux demi-grands axes, tel qu’il a été défini (hauteur relative au sommet opposé à C égale à la base) entraîne que le double de sa surface 2 ⋅ S est égale à la base élevée au carré. Soit, si d désigne la base (orbite inférieure à la suivante) : 2 ⋅ S = d2. Et de d2 on déduit la force centrale (accélération) exercée par le Soleil sur la planète [15]. Les rapports des forces centrales aux distances d des demi-grands axes sont donc comme les rapports des surfaces des triangles (voir note) et leurs rapports conduisent aux sinus élevés au carré des mêmes angles de la figure 1. C’est la première fois où un modèle de l’électromagnétisme fondé sur les nombres entiers, s’associe à un modèle gravifique également lié à des nombres entiers élevés au carré pour les planètes aux orbites relativement stables. Une relation inédite entre électromagnétisme et gravitation, chaperonnée par les nombres entiers, pour les données du système solaire et des orbites principales.
Du côté des planètes, nous avons évacué le problème des rapports de longueurs, transformables en rapports d’accélérations. Qu’en est-il du côté des énergies, longueurs d’ondes, etc. de l’atomistique ? Prenons la partie principale, le corps de la formule d’une fréquence, à savoir le résultat d’une soustraction d’un nombre fractionnaire par un autre nombre fractionnaire (fractions formées de nombres entiers, pythagoriciens par excellence). Soit, une transition entre les niveaux 2 et 3, on a, indépendamment de la constante R∞ [16] :
1/4 − 1/9 = 0,25 − 0,111 = 0,139.
En réduisant les fractions au même dénominateur, on a le même résultat avec (9 − 4) / (4 × 9) = 5 / 36… ce qui exprime un rapport entre les deux nombres entiers précédents élevés au carré (22 et 32). Si bien qu’une orbite de racine carrée de 5 divisée par une autre de racine carrée de 36, soit 2,236… / 6 = 0,3726… renverrait, selon la méthode des rapports, a un sinus de 21,88°… dont quelque amateur de nombres peut trouver rapidement la relation avec les entiers 4 et 9. Pour les données réelles du système solaire, la relation avec les nombres entiers a demandé plus de temps parce qu’il fallait additionner les angles et passer par les cotangentes des demi-angles avant de rejoindre les formules d’un pythagoricien clandestin. Un cheminement dans la globalité paraît toujours plus compliqué. Il n’y a pas qu’un seul chemin ; tous ne mènent pas à Rome.
Il ressort qu’un système constitué de rapports de nombres entiers est bien indiqué pour révéler des rapports identiques dans un autre système, si ces rapports existent. On démine avec un démineur, on ne va pas à la pêche à la baleine avec un filet à papillons. Une grille doit être adaptée à la sélection recherchée, et lorsqu’elle ne l’est pas, au lieu d’une baleine on attrape un papillon.
Les entiers naturels se retrouvent, de 1 à 4, dans le coefficient 4,48 égal à 16 fois 0,28… lequel est le rapport dit anharmonique ou birapport des nombres 12, 22, 32, 42, soit 1, 4, 9, 16 dans l’expression anharmonique :
(4 − 1) × (16 − 9) / (9 − 4) × (16 − 1)
3 que multiplie 7, à diviser par 5 que multiplie 15. Le résultat :
21 / 75 = 7 / 25 = 0,28 est égal à 4,48 / 16.
Curiosité ou relation numérique à approfondir, les premiers chiffres significatifs de la racine de 0,28 = 0,52915026 diffèrent peu du rayon de la première “orbite” circulaire de l’atome d’hydrogène, rayon de Bohr égal à 5,2917. 10−11 m. Tel un pythagoricien masqué, je pourrais adopter comme coefficient le rayon de Bohr élevé au carré (5,29177 × 10−11 m)2 multiplié par 16. Soit : 0,280029 × 10−20 × 16 = 4,48045… × 10−20. Le rayon du cercle de la figure 1, égal au premier rayon de Bohr, devient microcosmique, sans modification des angles au centre, indicateurs de directions spatiales et non des distances réelles des demi-grands axes.
Conformément à la Table d’Émeraude d’Hermès Trismégiste, le macrocosmique planétaire serait-il le fidèle reflet du microcosmique ? Sûrement pas. Les nombres entiers de la symbolique n’admettent pas de décimales, ni de valeurs approchées. Les signaux sont relatifs, réels, complexes ; imparfaits devant les symboles absolus, idéels, simples. Aussi, la communication entre symboles et signaux est-elle féconde en malentendus dans le mésocosme des humains. D’aucuns la croient impossible… comme si Dieu ne communiquait pas avec le Diable dans le dos des humains ?!
Les inverses des entiers 1 à 4, percent sous les sommes des cotangentes couplées. Sans coefficient anharmonique, les inverses de 4 et 5 apparaissent avec les différences des mêmes cotangentes.
Différences des cotangentes des demi-angles :
| Couple |
cot(Ân / 2) − cot(Ân′ / 2) |
| Jupiter - Cérès |
0,250 − 0,036 = 0,214 |
| Saturne - Mars |
0,589 − 0,340 = 0,249 |
| Uranus - Terre |
1,015 − 0,818 = 0,197 |
| Neptune - Vénus |
2,168 − 1,916 = 0,252 |
Alternance, oscillation que l’on peut arrondir à la fraction 1/5 pour Jupiter-Cérès et Uranus-Terre, à la fraction 1/4 pour Neptune-Vénus et Jupiter-Cérès.
Dans le système réel la cotangente du demi-angle correspondant à la position de Jupiter est égale à 0,25 (valeur arrondie) et la tangente du demi-angle correspondant à la position de Mercure égale à 0,21. En trigonométrie, la tangente est l’inverse de la cotangente [17]. Les différences des cotangentes couplées renvoient donc alternativement à 1/4 et 1/5 ou tangente Mercure et cotangente de Jupiter. Une oscillation entre deux entiers ou deux angles qui conduit à considérer Mercure et Jupiter comme les deux pôles de l’axe de la figure 1. Observation trigonométrique en faveur de l’homogénéité du système et de la fermeture du cercle. Mercure et Jupiter paraissent également liés à l’énigmatique 4,96… objet de cette mise à jour à l’occasion de la découverte de Sedna.
Pour Jupiter ce nombre concerne son périhélie, en “résonance” ou moyenne géométrique des périhélies de quatre orbites couplées de part et d’autre de sa position sur le cercle de la figure 1. Pour Mercure, outre le produit de son périhélie avec celui de Sedna égal à 4,962, son demi-grand axe peut se calculer par : 2 / (4,96 + 1/4,96) = 0,38748… au lieu de 0,387 1).
Cette opération n’a rien de cabalistique. Elle applique une formule de relation entre le sinus d’un angle et la tangente + la cotangente du demi-angle, soit sinus a = 2 / cot(a / 2) + tan(a / 2). Pour avoir 0,387 1, sinus de 22,774°… il faut donc prendre la cotangente de 22,774° / 2 = 11,387°. Soit : 4,9652… Ce nombre obstiné va réapparaître dans les cinq couples planétaires obtenus par les moyennes de leurs cotangentes.
On commence par les différences des positions sur le cercle de la figure 3 (cf. page 281). On note le sinus de l’angle correspondant à la différence entre deux positions consécutives.
| Différence des positions (°) |
Sinus |
| 52,21 − 0 = 52,21 M̂ |
0,790 m |
| 95,04 − 52,21 = 42,833 N̂ |
0,679 n |
| 130,2 − 95,04 = 35,16 Ô |
0,576 o |
| 163,75 − 130,2 = 33,55 P̂ |
0,552 p |
| 2 × (180 − 163,75) = 32,5 Q̂ |
0,537 q |
Les moyennes rendent les positions symétriques. De leurs angles identiques viennent, de droite à gauche, les mêmes sinus : une symétrie axiale qui efface les dissymétries de la figure 1. J’ai qualifié d’idéales les distances résultant de cette perfection. Idéales ne veut pas dire inventées : les demi-grands axes réels s’en déduisent par la formule des différences. En langage moderne, le système réel de la figure 1 est une “symétrie brisée” de la figure 3. Répondre à quand et comment une symétrie parfaite se brise et devient imparfaite n’est pas de ma compétence. J’ai néanmoins conscience d’exposer par deux figures géométriques accessibles à tous les cerveaux droits une brisure de symétrie imagée que les équations abstraites rendent peu compréhensible.
En partant de Pluton, 39,59 UA pour une position à 0°, le produit de 39,59 par 0,790… sinus de 52,21° détermine le demi-grand axe “idéal” de Neptune. Le produit Neptune × sinus n détermine le demi-grand axe “idéal” d’Uranus. Ainsi de suite, jusqu’à Mercure.
Les données, angles et sinus, ne justifient guère que trois ou quatre chiffres significatifs. Néanmoins, du début à la fin, j’ai laissé courir les 10 décimales de ma calculette pour n’arrondir que les résultats. De produit en produit, de sinus en sinus, on obtient, pour les planètes aux positions symétriques :
| Planète n |
Dn |
Planète n′ |
Dn′ |
| Pluton |
39,59 |
Mercure |
0,622 |
| Neptune |
31,27 |
Vénus |
0,787 |
| Uranus |
21,26 |
Terre |
1,159 |
| Saturne |
12,25 |
Mars |
2,012 |
| Jupiter |
6,77 |
Cérès |
3,64 |
En calculant la moyenne géométrique de chaque couple comme pour les périhélies, aphélies et demi-grands axes du système réel, nous voyons resurgir 4,963 …
| Couple |
Dn × Dn′ |
| Pluton - Mercure |
39,59 × 0,622 = 24,633 = 4,9632 |
| Neptune - Vénus |
31,27 × 0,787 = 24,633 = 4,9632 |
| Uranus - Terre |
21,26 × 1,159 = 24,633 = 4,9632 |
| Saturne - Mars |
12,25 × 2,012 = 24,633 = 4,9632 |
| Jupiter - Cérès |
6,77 × 3,64 = 24,633 = 4,9632 |
La persévérance cardinale de ce nombre reste à expliquer. En revanche, il est facile de démontrer pourquoi des couples en symétrie donnent une constante, celle-ci ou une autre.
Pour cela, prenons en exemple le couple Jupiter-Cérès. Au lieu d’écrire : Saturne × sinus p → Jupiter → 6,74… nous avons le même résultat avec 39,59 (Pluton) × m × n × o × p → Jupiter → 6,74 … que l’on écrit plus commodément 39,59 m ⋅ n ⋅ o ⋅ p. → Jupiter. Laquelle écriture devient 39,59 m ⋅ n ⋅ o ⋅ p ⋅ q, pour Cérès…
Le produit Jupiter × Cérès s’exprime donc par :
39,592 ⋅ m2 ⋅ n2 ⋅ o2 ⋅ p2 ⋅ q … égal à 24,633… ou 4,9632.
et il en sera de même pour les autres couples qui, avec des valeurs différentes renvoient, du fait de leur symétrie, à la même constante.
Observons que celle-ci s’écrit aussi :
(39,59 ⋅ m ⋅ n ⋅ o ⋅ p)2 × q = 4,9632
et que : (39,59 ⋅ m ⋅ n ⋅ o ⋅ p)2 = Jupiter2 = 6,742 …
la constante passe alors du côté de Jupiter avec :
Jupiter2 × q = 6,772 × sinus de 32,5° = 24,63 = 4,962.
Voilà une explication plausible et chiffrée de la moyenne géométrique du système solaire de 5,342 proche du demi-grand axe de Jupiter. La fluctuation des produits des couples planétaires autour de son demi-grand axe vient du fait que les angles de part et d’autre de sa position ne sont pas exactement symétriques.
Pour que les angles de la figure 3 le soient, il faut diviser par 2 l’angle de 32,5°. La partie gauche, partie des planètes rapides (par convention) devient la réplique de la partie droite des planètes lentes. Le demi-angle de 32,5° → 16,25° a pour sinus : 0,2798… qui restitue le rapport anharmonique des nombres 1, 4, 9, 16. Indépendamment de toute hypothèse de relation avec les transitions de l’hydrogène, tel l’éléphant d’Alexandre Vialatte, la préséance des entiers 1 à 5 dans le système solaire est irréfutable. La dernière relation réduit le problème de la répartition des orbites à des équations de trigonométrie pure, puisque l’on peut prendre comme coefficient, pour le système idéal ou générateur du système réel : 16 fois le sinus de 16,25°.
Le nombre 4,96 se distingue par sa relation avec l’angle de 22,8° dont le sinus correspond au demi-grand axe de Mercure. Il ne se déduit pas des nombres entiers, mais il occupe le terrain avec un bilan impressionnant :
- Périhélie de Jupiter, dominante du système solaire actuel.
- Moyenne géométrique des périhélies des couples planétaires de part et d’autre de Jupiter dans le système solaire actuel.
- Moyenne géométrique des périhélies de Mercure et Sedna.
- Moyenne géométrique de tous les couples planétaires du système idéal (ou originel) inféré par les moyennes des cotangentes des demi-angles au centre du système solaire actuel.
À ce score s’ajoute celui qui, peut-être, donne la clef de ces performances : la distance 4,96 UA correspond à un cycle de 11,05 ans… cycle moyen de l’activité solaire, le soleil étant une boule d’hydrogène… dont on n’a pas trouvé (il y a des hypothèses) les raisons précises de son cycle d’activité.
Attendre le mathématicien qui saura corriger les positions réelles ?
Si cette relation est correcte, les tentatives de corréler les positions planétaires du système réel-actuel à l’activité solaire et son cycle moyen de 11 ans risquent d’être à la fois attractives et vouées à l’échec. Pour avoir une bonne corrélation, il faudrait que le système idéal soit le système réel… or, nous avons constaté, autant par les images que par les nombres, que le système réel est une symétrie brisée. Avec le cycle solaire, on n’en tirera jamais que des corrélations fragmentaires. Ou alors, il faut attendre le mathématicien qui saura corriger les positions réelles ? Je ne sais ni qui, ni comment.
Autre problème que la découverte de Sedna aide à résoudre. Après une fermeture du cercle par Mercure ou Pluton, peut-on envisager un nouveau tour… une autre suite de planètes au-delà de Pluton, plutôt qu’entre Mercure et le Soleil ? Sedna répond non. Les angles étant déterminés par les rapports (sinus) des demi-grands axes, en divisant 39,6 par le demi-grand axe approximatif de 500 UA de Sedna, on obtient 0,079… sinus d’un angle de 4,5°. Sedna n’embraye pas un nouveau tour de spirale ; elle reste sensiblement dans la même direction que Pluton. Sa candidature au rang de planète à part entière est rejetée, malgré un périhélie qui témoigne d’un attachement partiel ou d’une origine commune. Je peux donc réitérer l’option énoncée dans plusieurs articles et dernièrement dans les Cahiers no 28 :
“Quelles que soient les raisons de fermer le cercle, ce n’est pas le seul argument, nous l’avons vu, en faveur d’un système homogène excluant un ajout sans règle. L’axe Jupiter-Mercure mis en valeur par les couples appariés, nécessite, pour qu’on suive la règle, une orbite avant Mercure si l’on en prend une après Pluton ; une orbite après Pluton si l’on en prend une avant Mercure. Contrainte délicate à respecter pour entrer dans le clan ; si elle évacue les orbites qui n’y adhèrent pas, elle n’interdit pas les marginales. ” (Je souligne).
Il n’est pas davantage interdit aux astrologues de se précipiter sur les éphémérides de Sedna pour en faire une relance de leurs chiffres d’affaires, remanier les maîtrises, continuer à se moquer du monde, faire des statistiques et des indices cycliques et mettre le conditionalisme sectaire à l’index.
FIGURE 3 - Les moyennes des cotangentes des demi-angles au centre des figures 1 et 2 déterminent de nouvelles positions sur le cercle de 360°. Les différences consécutives déterminent de nouveaux angles au centre m, n, o, p, q. En partant de Pluton 39,59 UA, les sinus de ces angles donnent les demi-grands axes d’un système idéal d’une symétrie parfaite.
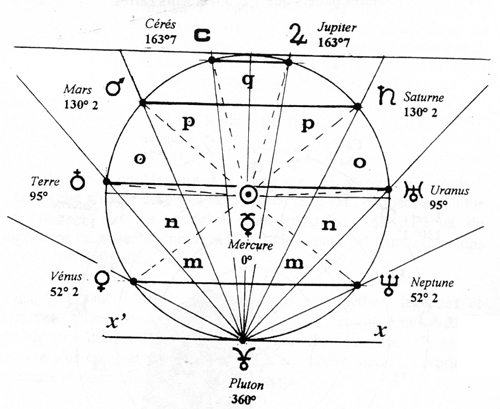
On connaît la spirale d’Archimède, les spirales logarithmique et hyperbolique. Cette dernière figure permet de tracer une spirale inédite en portant sur chaque direction ou rayons successifs les valeurs données par les sinus des angles. Soit, une longueur arbitraire ou égale à 1 pour un exemple simple. Si l’on part du rayon perpendiculaire à l’axe des x, on porte la longueur 1, puis 1 × m (sinus de m) sur le rayon qui suit, selon le sens inverse des aiguilles d’une montre (ou sens direct en astrométrie). Le troisième rayon aura la longueur de 1 × m ⋅ n…, le quatrième 1 × m ⋅ n ⋅ o… jusqu’à la fin du cercle ou d’un cycle qui peut recommencer indéfiniment comme le font les spirales géométriques. Bien entendu, on peut partir du côté gauche et suivre cette fois, le sens des aiguilles d’une montre tout en multipliant la longueur initiale par les sinus consécutifs. Enfin, on peut partir de n’importe quel rayon comme de n’importe quelle longueur, en sachant que pour avoir des longueurs supérieures à l’unité choisie, il faut diviser par les sinus des angles au centre et pour les longueurs inférieures il faut multiplier.
Indépendamment de toute référence à l’astrométrie ou à la physique, il est possible d’étudier les spirales obtenues comme celle-ci par d’autres nombres entiers que 1, 2, 3, 4 et leurs carrés.
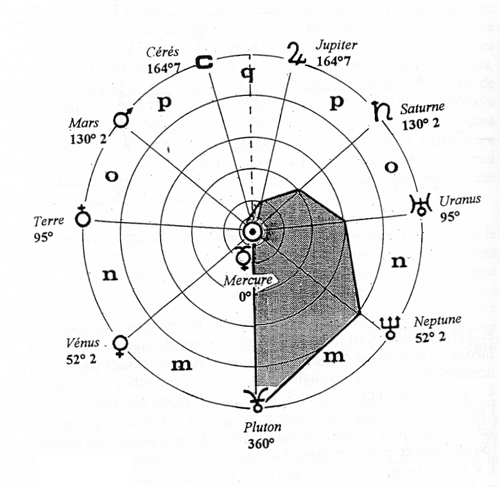
Revenons maintenant à la théorie (texte de Sir Arthur Eddington)
“Le savant professe communément qu’il fonde son opinion sur des observations et non sur des théories. Les théories, dit-on, sont utiles en ce qu’elles suggèrent à l’expérimentateur des idées nouvelles et de nouvelles directions de recherche ; mais les ‘faits bruts’ constituent la seule base correcte pour tirer des conclusions. Je n’ai jamais fait obstacle à quiconque met en pratique cette profession de foi — mais ce n’est sûrement pas l’expérimentateur borné qui est d’autant plus influencé par ses théories qu’il est moins accoutumé à les examiner. L’observation ne suffit pas. Nous croyons nos yeux qu’autant que nous avons la conviction préalable que ce qu’ils semblent nous apprendre est croyable. (Je souligne).
“Il est préférable d’admettre franchement que la théorie a, et est qualifiée pour avoir, une part importante dans la détermination de notre jugement. Pour le lecteur résolu à fuir la théorie et à n’admettre que des faits d’observation précis, tous les livres d’astronomie sont à bannir. Il n’y a pas, en ce qui concerne les corps célestes, de faits d’observation purs [soulignement de Sir Eddington]. Les mesures astronomiques sont toutes, sans exception, des mesures de phénomènes qui se passent dans un observatoire ou une station terrestre ; ce n’est que grâce à la théorie que ces mesures peuvent être traduites en connaissance d’un univers extérieur.” (Je souligne). [18]
Voilà le texte d’un scientifique de haut niveau qui ne fera certes pas fléchir la morgue des “praticiens” anti-édifice collés à leur glose symbolo-magiste. Tout ce qu’écrit Sir Eddington à propos des “faits d’observation” en astronomie peut s’appliquer aux faits d’observation statistiques ou cliniques de l’astrologie. Devant ces faits, qui témoignent sans exception, de la relativité de l’astrologie, la théorie du symbolisme absolu en opposition au signal absolu, est inadéquate. L’Homme n’est pas le reflet de son ciel. En revanche, la théorie conditionaliste, de la relation signal-symbole, qui s’est déjà révélée féconde pour les fondements de l’astrologie, ouvre à une nouvelle et plus large compréhension du symbole comme du signal.
Bibliographie
- Ciel et Espace. Mai 2004. Article de Azar Khalatbari : Sedna est-elle la dixième planète ?
- Emmanuel Lellouch, spécialiste des atmosphères des planètes lointaines à l’Observatoire de Paris-Meudon. Ciel et Espace de mai 2004.
- Cahiers conditionalistes no 2. Article : L’ordre solo-planétaire. COMAC. 3e trimestre 1980.
- Nombres et Formes du Cosmos. Recueil d’articles. Publié en 1971 à compte d’auteur. Opus cité.
- Pour une astrologie moderne. Opus cité.
- Matière, Terre et Ciel (trois tomes). Georges Gamow. Traduction Geneviève Guéron. Dunod. Paris. 1961. Le livre est ancien, mais j’ai préféré confier l’explicative des raies spectrales à un grand physicien.
- Les secrets de la matière. Helmut Carl. Traduit de l’allemand par Philippe Florent. Union Générale d’Éditions. 1963. Paris.
- La Bosse des maths. Stanislas Dehaene. Éd. Odile Jacob. Paris. 1997.
Article paru dans le no 29 des Cahiers conditionalistes. (4e trimestre 2004)
Article suivant — Introduction à la cosmogonie astrologique
[1] Tg = 2 ⋅ π ⋅ √(L / g). Avec : Tg : période d’oscillation ; L : longueur du pendule ; g : intensité de la gravité au lieu où bat le pendule.
[2] “Ainsi la science est beaucoup plus proche du mythe qu’une philosophie scientifique n’est prête à l’admettre. C’est une des nombreuses formes de pensée qui ont été développées par l’homme, mais pas forcément la meilleure. La science est indiscrète, bruyante, insolente ; elle n’est essentiellement supérieure qu’aux yeux de ceux qui ont opté pour une certaine idéologie, ou qui l’ont acceptée sans avoir jamais étudié ses avantages et ses limites.” (Paul Feyerabend, Contre la méthode, Seuil 1975).
[3] Cette constante dépend des unités choisies. En système international (SI) qui emploie le mètre, le kilogramme et la seconde, elle s’écrit : 6,672 × 10−11 m3 ⋅ kg−1 ⋅ s−2 (Bureau des Longitudes. 1997). La détermination expérimentale de G fut réalisée pour la première fois en 1798 par Henry Cavendish (1731–1810). Né le 10 octobre 1731 à Nice, H. Cavendish a illustré son Signe solaire par sa célèbre balance de torsion, appareil ingénieux grâce auquel il a déterminé la valeur de G le plus simplement du monde.
[4] La Gravitation (Georges Gamow. Petite Bibliothèque Payot. 1963)
[5] La Terre et le pendule. (F. Boubleinikov. Éditions en langues étrangères. Moscou 1961).
[6] Mikhaïl Vassilievitch Lomonossov. Écrivain et savant russe. Né le 8 (19) novembre 1711, mort le 4 (15) avril 1765. Si vous ne trouvez pas sa biographie dans Tintin chez les Soviets, consultez le Nouveau Dictionnaire des Auteurs (Robert Laffont. 1994).
[7] Pour avoir 1, il faut négliger la masse m de la planète devant la masse M3 du Soleil, compter la distance en UA et la période en année et/ou fraction d’année. En unités SI on écrit : L3 / T2 = G ⋅ (M3 + m) / (4 ⋅ π2) où G est la constante de gravitation universelle. Il saute aux yeux que si m de chaque planète est trop important pour être négligé, J. Kepler ne connaissant pas les masses planétaires aurait eu du mal à trouver sa 3e loi (sans parler des trajectoires). Ce n’est pas l’avis de Mouchassieux qui réprimande ma remarque. Les effets psychomentaux de l’anti-astrologie sont décidément désastreux.
[8] L’ex-association l’ARRC, le RAMS, le GERASH, le CURA qui placent un ‘R’ dans leur sigle pour évoquer un objectif de recherches n’ont manifesté aucun intérêt pour cet appel. Puisque ces Associations n’ont d’autre idéal déclaré que la réalité, qu’elles dressent donc leur bilan comme nous avons dressé le nôtre pour rendre les comparaisons possibles et instructives.
[9] T2, Révolution sidérale ; f3, force centrale (exercée par le Soleil) ; g, intensité de la pesanteur à la surface ; Tg2 période (théorique dans cette recherche) déterminée par la formule du pendule simple : Tg2 = 4 ⋅ π2 ⋅ L / g.
[10] Étoile pulsante, dont l’étoile δ Céphée est le prototype et dont l’éclat varie suivant une période bien déterminée, s’échelonnant entre un jour et quelques semaines. (Ph. de la Cotardière. Dictionnaire de l’astronomie. Larousse. 1987)
[11] 5,32 UA = moyenne géométrique des demi-grands axes des planètes principales, à l’exception de Mercure, mais Pluton compris. Proche de cette distance : 4,96 UA : périhélie de Jupiter et, d’après la 3e loi de Kepler, distance correspondant au cycle moyen de l’activité solaire, 11,05 ans.
[12] f3 = accélération déterminée par la distance au Soleil. g = accélération déterminée par la distance au centre de la planète.
[13] Article de Daniel Wells dans Fusion no 86 de mai-juin 2001.
[14] Formule du moment d’inertie d’une masse tournant autour de son axe : I = M ⋅ R2 / 2.
[15] Constante héliocentrique de gravitation = G ⋅ M3. L’accélération centrale, en négligeant la masse de la planète à la distance d, s’exprime par f3 = G ⋅ M3 / d2. Le double de la surface du triangle dont la base d est opposée à une hauteur égale à la base est égale à 2 ⋅ S = d2. Il vient que G ⋅ M3 / (2 ⋅ S) = G ⋅ M3 / d2 = f3.
[16] Constante « infinie » de Rydberg. En SI (système international) : 1,097 37 × 107 m−1
[17] Soit un angle 14,036°… Les tables (et les calculs) indiquent que la cotangente correspondant à cet angle est 4. La tangente du même angle est 1 / 4 = 0,2.
[18] L’Univers en expansion. Sir Arthur Eddington. Traduit de l’anglais par J. Rossignol. Hermann et Cie Éditeurs. Paris. 1934.