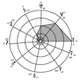
Organisation des demi-grands axes des orbites principales
Le lecteur averti aura reconnu dans la formule des cotangentes significatives pour le système solaire, un sérieux air de famille avec celle, découverte par Johann Jakob Balmer (1825–1898), physicien et ésotériste pythagoricien. Pour relier harmonieusement les longueurs d’onde des neuf raies alors connues du spectre d’émission de l’atome d’hydrogène, J. Balmer, en 1885, proposa :

Avec k = 3 645,6 ångströms et m entier variant de 3 à 11. Aujourd’hui, cette constante pour la série de Balmer n’a guère été corrigée (3646 Å), et l’on a adopté la forme proposée par le physicien suédois Johannes Robert Rydberg (1854–1919) :

L’inverse de la longueur d’onde, exprimé en mètres, est le nombre d’ondes (par mètre dans le vide) de la radiation considérée. RH est la constante de Rydberg qui, pour l’atome d’hydrogène, est égale à 1,096 776 × 107 m−1.
Le calcul théorique de cette constante met en jeu une masse nucléaire qui tendrait vers l’infini R∞, et le rapport de la masse de l’électron au repos me, avec la masse du proton dans le même état mp, de façon que :

Aucun ouvrage d’enseignement non-spécialiste ne s’appesantirait sur ces détails. Je l’ai fait, jusqu’ici, en démenti aux schatzmanicheens pour qui les astrologues n’ont droit ni au langage, ni à l’étude des sciences… exactes, au prix d’une manipulation des nombres et des puissances dont on aimerait mieux connaître la rationalité, surtout quand on est mis sans procès, au big-ban de la raison dominante. En attendant le jour ou les astrologues désaliénés du magico-symbolisme seront suffisamment adultes pour exiger des explications tant de leurs gourous que de leurs exorcistes, que les lecteurs impatients veuillent bien se reporter à la bibliographie [1] pour le contexte des définitions de l’atomistique.
Lorsqu’on a une longueur d’onde et la dernière mesure connue de la vitesse de la lumière c = 299 792 458 m ⋅ s−1, on en déduit la fréquence :

Multipliée par le quantum d’action de Planck (1848–1947) ℎ = 6,626 × 10−34 J ⋅ s (Joule ⋅ seconde), le produit donne une énergie : E = ℎ ⋅ f… que l’on exprime en électronvolts en divisant ℎ ⋅ f par la charge électrique élémentaire e = 1,602 × 10−19 C (Coulomb). En résumé, de l’équation :

découle la longueur d’onde associée à 1 eV :

que l’on exprime en unités S.I. : 1,24 × 10−6 m.
Tout bouge en mécanique ondulatoire, mais il est toujours possible de définir l’état de l’électron dans un atome par un minimum provisoire de quatre nombres quantiques : n (nombre quantique principal) ; l (nombre quantique orbital) ; m (nombre quantique magnétique) ; s (nombre quantique de spin). Avec des règles de combinaison et d’exclusion, ces nombres permettent de retrouver les longueurs d’ondes et niveaux d’énergie d’atomes à couches électroniques multiples. Leur point commun serait d’être des entiers absolus ou relatifs ; des entiers simples, le plus souvent à la deuxième puissance.
À des fins pédagogiques démonstratives, les théories de l’atomistique s’enseignent en partant du modèle de l’hydrogène (1 noyau, 1 électron) et du nombre quantique n en rapport principal avec les différentes valeurs d’énergie de l’atome. Le modèle ressemble à la réalité autant qu’un dessin de chameau à son odeur. Il n’y aurait pourtant rien à reprocher à ceux qui en usent s’ils avaient envers les modèles astrologiques, reflets imparfaits de l’invisible, autant de tolérance que pour les leurs.
L’étude des spectres d’émission de l’atome d’hydrogène a permis de trouver les niveaux possibles de l’énergie E. En électronvolts :

Pour n = 1, E1 = −13,6 eV. Niveau d’énergie minimal (correspondant à l’état stationnaire fondamental).
Pour n plus grand que 1, l’énergie correspondante est comprise entre 0 et −13,6 eV. L’atome est dans l’un des états excités. On disait autrefois, en langage imagé, qu’il avait changé d’orbite. L’énergie d’un atome excité est supérieure à celle de l’atome à l’état fondamental. En grandeur relative, une énergie de −0,066 est en effet supérieure à −13,6.
Pour n infini, E = 0. L’atome est dans l’état ionisé, l’électron e− est séparé du noyau H+. Il est libre. Les niveaux d’énergie se resserrent avec les grandes valeurs de n. lIs deviennent indiscernables pour les très grandes valeurs, d’où la convention de E = 0 lorsque n tend vers l’infini.
La collision d’un atome avec une autre particule ou avec un quantum assez dur peut exciter ou ioniser l’atome, c’est-à-dire faire passer l’électron à un niveau supérieur ou à l’état libre. Les énergies quantiques à fournir pour exciter ou ioniser un atome sont relatives. Elles diffèrent selon les niveaux et, par conséquent, selon l’état où l’atome se trouve déjà. Ainsi, le potentiel d’excitation du deuxième niveau de l’atome d’hydrogène est de 10,12 eV (n = 2), et le potentiel d’ionisation à partir du premier niveau de 13,6 eV (n = 1). L’énergie du quantum ionisant peut être sensiblement plus grande que le potentiel d’ionisation nécessaire. En ce cas, l’électron éjecté se déplace à la vitesse v, que l’on calcule d’après l’équation photoélectrique :

In désignant le potentiel d’ionisation considéré.
Un atome excité revient à son état fondamental par transitions directes ou successives qui s’accompagnent d’une émission de photons. À l’état excité, la durée moyenne de présence de l’électron au niveau n est théoriquement proportionnelle à n élevé à la 5e puissance. Soit, sensiblement :

Le temps moyen d’existence d’un atome à l’état ionisé se calcule par une autre équation mettant en cause la concentration des électrons libres et la température du plasma.
Une transition depuis un état excité Eq vers un état Ep qui l’est moins (p < q), s’accompagne de l’émission d’un photon d’énergie :

Émission à laquelle correspond une longueur d’onde de :

L’ensemble des raies qui constituent le spectre d’émission de l’atome d’hydrogène est classe en séries, une série correspondant aux transitions qui aboutissent au même niveau d’énergie. La série de Balmer comporte les raies de transition aboutissant au niveau p = 2, avec q > 2 = 3, 4, 5, 6… Elle comprend 4 raies représentatives de l’hydrogène optique et coloré :
q
|
Raie
|
Couleur
|
Longueur d’onde
(Å) |
| 3 |
Hα |
rouge |
6564 |
| 4 |
Hβ |
vert-bleue |
4862 |
| 5 |
Hγ |
indigo |
4341 |
| 6 |
Hδ |
violette |
4102 |
La série s’étend dans l’ultraviolet avec des lignes de plus en plus serrées jusqu’à la limite, vers 3 640 Å. Sur la trace de Balmer, d’autres séries ont été découvertes :
- Ultraviolette de Lyman (1906) : Retour au fondamental p = 1
- Infrarouge de Paschen (1909) : Retour au niveau p = 3
- Infrarouge de Brackett (1922) : Retour au niveau p = 4
- Infrarouge de Pfund (1924) : Retour au niveau p = 5
Autant de retours schématisés dans la Fig. 8 pour un spectre d’émission. un phénomène d’absorption apparaît comme rigoureusement réciproque au phénomène d’émission : il suffit de changer le sens des transitions. Il ne manquait à ces raies historiques en séries, que la série planétaire… constituée, à l’inverse des précédentes, d’un départ commun (niveau q = 4) et d’arrivées (p = 1, 2, 3). Le couple Jupiter-Cérès entre dans le système avec la transition du niveau 8 à 7. Pour Mercure, il faudrait changer d’atome-modèle… Nous ne sommes qu’au début de cette approche.
Formellement, les entiers p et q ayant, pour l’hydrogène, la constante de 13,6 eV, et pour les cot2 planétaires, le nombre sans dimension de 2,11662, le rapport 13,6 / 4,48 = 3,036 suffit pour passer des rapports des demi-grands axes planétaires aux niveaux d’énergie, sans qu’il y ait, a priori, preuve de relation physique directe. Présomption d’un lien, seulement.
Pour les longueurs d’onde, exprimées en ångströms, on multiplie les tangentes au carré par 911 Å × 4,48 = 4 081. Ces coefficients varient selon les unités utilisées pour exprimer les énergies, longueurs d’ondes et distances. Les définitions des transitions par les entiers p et q, restent inaltérées. L’important serait donc de savoir quelle est l’unité de distance à adopter pour les planètes, s’il y a en une qui peut rendre l’ensemble homogène. Avec les ångströms, eV, et 2,11662 sans dimension, pour connaître la série des correspondances planétaires, commençons par le tableau des énergies de chaque niveau :
TABLEAU IX — Énergies (eV) pour les niveaux n, et longueurs d’onde (Å) pour les transitions de n + 1 à n.
Énergie
En (eV) |
Longueur d′onde
λn + 1→n (Å) |
| E1 = −13,6 |
de 2 à 1 = 1 215 |
| E2 = − 3,4 |
de 3 à 2 = 6 560 |
| E3 = − 1,52 |
de 4 à 3 = 18 748 |
| E4 = − 0,85 |
de 5 à 4 = 40 502 |
| E5 = − 0,54 |
de 6 à 5 = 74 560 |
| E6 = − 0,38 |
de 7 à 6 = 123 656 |
| E7 = − 0,28 |
de 8 à 7 = 190 522 |
| E8 = − 0,21 |
de 9 à 8 = 277 892 |
Les longueurs d’ondes indiquées ne concernent donc que les transitions successives.

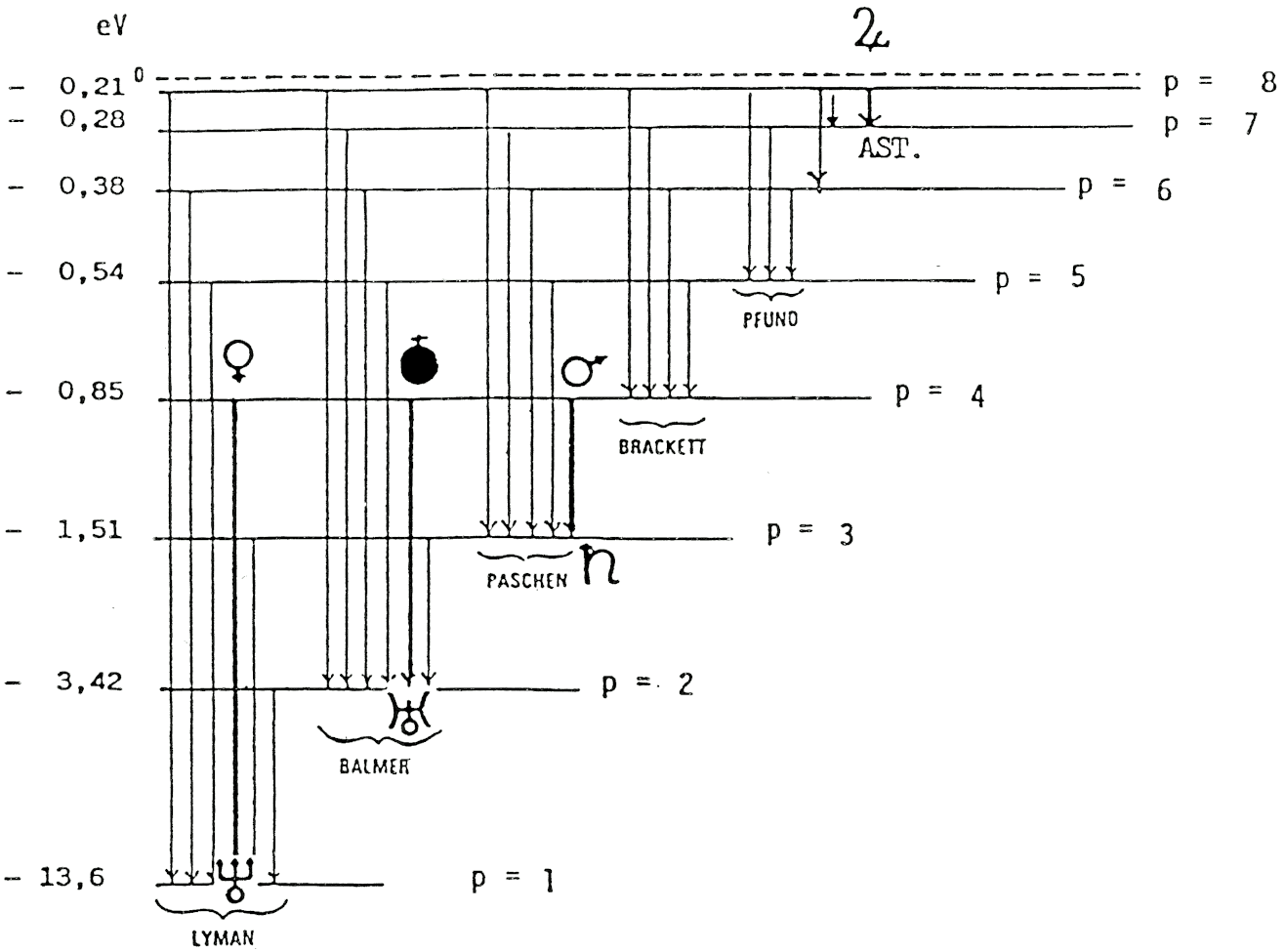
FIG. 8 — Schéma des transitions pour les niveaux de : p = 8 à p = 1 (fondamental), selon le nombre quantique principal. Ne figurent pas les transitions contiguës déterminées par l’interaction spin-orbite qui décompose les niveaux d’énergie et sépare chaque raie en multiplets de structure fine (doublets pour les atomes à un électron). En revanche, de façon inédite, figurent en gras les transitions qui conduisent aux valeurs des cot2(Ln / 2) déterminées par les rapports des demi-grands axes planétaires. Soit :
TABLEAU X — Longueur d’onde correspondant aux couples planétaires selon la règle des transitions q→p.
Couple
|
Transition
q→p |
Eq − Ep = Eq→p
(eV) |
λq→p
(Å) |
| Jupiter - astéroïdes |
8→7 |
−0,214 − − 0,279 = 0,065 |
190 500 |
| Saturne - Mars |
4→3 |
−0,853 − − 1,517 = 0,664 |
18 746 |
| Uranus - Terre |
4→2 |
−0,853 − − 3,413 = 2,56 |
4 860 |
| Neptune - Vénus |
4→1 |
−0,853 − −13,65 = 12,797 |
975 |
Comme l’exigent les critères d’objectivité, ces calculs sont renouvelables en tous temps et tous lieux par des expérimentateurs différents. À quelques ångströms près, les résultats seront identiques. Il n’a été introduit aucun artifice. Mais, en présence de correspondances inattendues, on doit se demander s’il s’agit d’analogies, de relations logiques ou artificielles. Est-on en droit d’associer des énergies à des longueurs ? L’atomistique le fait… avec des précautions. J’ai pris celles de souligner que les distances moyennes (demi-grands axes) étaient représentées par une suite de triangles, un éventail de surfaces sans lesquelles aucune de ces relations n’apparaîtraient. Malgré tout, si l’on préfère les longueurs d’ondes aux niveaux d’énergie, le recours aux tangentes plutôt qu’aux cotangentes aboutit aux mêmes relations.
Que penser de l’ordre de grandeur des unités comparées ? Une unité astronomique est 1021 fois plus grande que l’ångström. Malgré leur loi commune en inverse carré (1 / R2), la force de gravitation est 1040 fois plus faible que l’intensité de l’attraction électrostatique. Mais si l’on considère les accélérations, celle qu’exerce le Soleil sur Jupiter, autour de 0,000 22 m ⋅ s−2, est seulement 10 fois supérieure à la longueur d’onde attribuée au couple Jupiter-astéroïdes dans le tableau X. Quant aux accélérations exercées par les planètes sur le Soleil, elles sont de l’ordre du micron (10−6 m), comme la longueur d’onde associée à l’intensité maximale du rayonnement d’un corps noir à la distance D (en UA) du Soleil et à la température, en kelvins, de 394 / √D selon l’expression approchée de la loi de Wien :

La comparaison invite à rechercher une explicative des effets planétaires dans l’interférence des forces de gravitation avec les rayonnements thermiques, optiques, dans des limites et des modes à préciser. Si la courbure de l’espace-temps se creuse à la distance Soleil-Jupiter, de 222 microns, on peut concevoir qu’une oscillation entretenue, sensiblement commensurable avec cette longueur, peut se composer avec elle, entraîner des phénomènes de résonance, d’occlusion ou d’amplification. Quelle que soit l’hétérogénéité des déterminismes, leurs effets peuvent se combiner. Pour l’explicative de l’astrologie dans ses principes et non ses mécanismes, la gravitation agirait comme une grille d’élimination ou de renforcement d’autres sources rayonnantes. Elle en serait le guide, la trame gagnant par la persistance ce qu’elle n’a pas en intensité.
En matière de température et gravité, les ondes et les accélérations centrales, bien que relevant d’équations différentes, ont le Soleil comme cause commune principale. Les longueurs issues des formules sont antisymétriques : les hautes énergies rayonnantes sont associées à de courtes longueurs d’ondes, les fortes attractions gravitationnelles accentuent la courbure de l’espace-temps ; l’onde de chute “seconde par seconde” est d’autant plus grande que l’attraction est forte. Il y a forcement une distance au Soleil où la longueur d’onde dominante d’une surface réceptrice-émissive idéale (corps noir) correspond à la longueur de chute (seconde par seconde) vers le Soleil.
Sachant que la température effective du Soleil est de 5 770 kelvins, une planète qui présenterait toujours la même face au Soleil et qui absorberait et émettrait comme un corps noir aurait une température conforme à la formule [2] ci-dessous :

Longueur d’onde dominante à cette température :

L’accélération centrale (f3) étant sensiblement de 0,0059 m ⋅ s−2 à la distance de 1 UA, pour avoir λm = f3, on pose :

Le quotient de 0,0059 / (7,36 × 10−6) soit : 802, indique la distance D élevée à la puissance 2,5 à laquelle λm = f3.
On trouve : D = 14,51 UA. Et l’on observe que √802 = 5,322. La constante des couples planétaires (tableau III) réapparaît. La figure 9 montre une relation plus logique, quoique moins précise, entre 5,32 et 15,04, axe de l’hyperbole obtenue avec les distances moyennes au Soleil.
La λm de Tp proportionnelle à √D est facile à calculer par la formule approchée ci-dessus. Autant en user pour comparer les couples planétaires dont la somme des rangs est égale à 8, à ceux dont la somme égale 9.
TABLEAU XI — Moyenne géométrique des λm par couples planétaires.
Couple
|
n
|
n′
|
λ × λ′
(µm) |
√(λ × λ′)
C = 9 C = 8 |
| Mercure - Pluton |
9 |
0 |
4,67 × 46,7 |
= 14,69 |
| Vénus - Pluton |
8 |
0 |
6,31 × 46,7 |
= 17,17 |
| Vénus - Neptune |
8 |
1 |
6,31 × 40,7 |
= 16,03 |
| Terre - Neptune |
7 |
1 |
7,43 × 40,7 |
= 17,34 |
| Terre - Uranus |
7 |
2 |
7,43 × 32,6 |
= 15,56 |
| Mars - Uranus |
6 |
2 |
9,16 × 32,6 |
= 17,28 |
| Mars - Saturne |
6 |
3 |
9,16 × 23 |
= 14,52 |
| Cérès - Saturne |
5 |
3 |
12,4 × 23 |
= 16,89 |
| Cérès - Jupiter |
5 |
4 |
12,4 × 17 |
= 14,53 |
| Jupiter |
4 |
|
(= 17) |
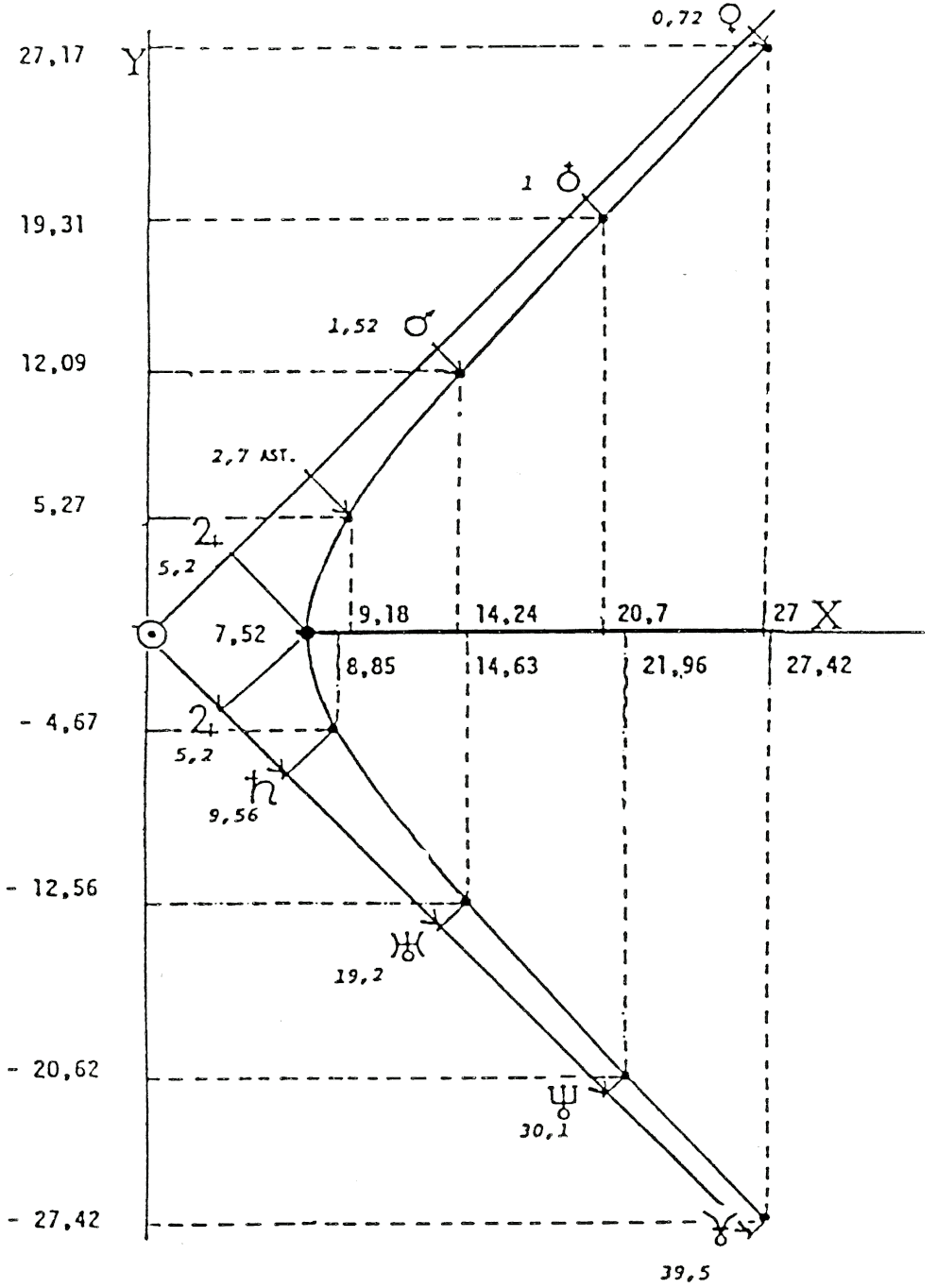
- Grand axe : 15,04
- Distance focale : 10,64
- Paramètre : 5,32
- Directrice : 5,32
FIG. 9 — La branche d’hyperbole génératrice des demi-grands axes des planètes principales, a 15,04 UA pour grand axe. Cette distance liée à la constante de 5,32 UA (paramètre et directrice de l’hyperbole) est proche de 14,6 où des formules différentes donnent des longueurs de même valeur numérique.
La série 9 est moins rigoureuse autour de sa constante (moyenne : 14,9) que la série 8 (moyenne : 17,14), en revanche, elle intègre le couple Mercure-Pluton.
Ces λm se déduisent des distances √D comme si les planètes n’opposaient au Soleil qu’une face absorbante immobile et sans fantaisie émissive. En réalité, il est bien connu qu’une planète tourne sur elle-même. Elle reçoit de l’énergie proportionnellement à sa surface apparente π ⋅ r2 mais, en tournant, elle rayonne une énergie proportionnelle à toute sa surface, égale à 4 ⋅ π ⋅ r2. Sachant que la puissance totale rayonnée par un corps noir dans toutes les longueurs d’onde et dans toutes les directions est proportionnelle à sa surface et à la quatrième puissance de sa température (loi de Stefan), entre une sphère fixe et une en rotation, le rapport des températures effectives est égal à la racine quatrième de 4, soit √2. Au lieu de Tp = 394 / √D, on adopte :

qui devient :

La moyenne des résultats passe à 14,9 × √2 = 21 microns pour les couples “9” ; à 17,14 × √2 = 24,24 microns pour les couples “8”. Selon la première formule, à la distance 14,5 UA la longueur d’onde dominante est de : 28 microns, valeur égale à l’attraction centrale à cette même distance. Des relations simples s’établissent entre 28 µm et les moyennes : 1/2 (21 + 28) = 24,5 µm. La relation : 28 / √2 = 19,8 µm… exigerait d’élever la température du Soleil ou de lui affecter un coefficient de lenteur. Pourquoi pas ?
Pour approcher davantage du réel, on distingue dans les rotations les vitesses lentes et rapides. Jupiter, Saturne, Uranus, Neptune, tournent sur eux-mêmes à des vitesses supérieures à 2 km/s (Jupiter : 12,34 km/s). Les vitesses linéaires de rotation de Mars, Terre, sont inférieures à 500 m/s, celles de Vénus, Mercure baissent au mètre/seconde, Pluton bien en-dessous. Pour ces astres, la correction est égale à la racine quatrième de 2 et non de 4… En outre, les planètes, selon la nature du sol et de leur atmosphère, n’ont pas le même pouvoir (albédo) de réflexion ou rediffusion de l’énergie reçue, et chaque astre a son albédo dans l’infrarouge, le visible, l’ultraviolet. Compte tenu de cette complexité, il est intéressant de connaître les √(λ × λ′) des couples planétaires à partir des températures les plus proches des mesures effectuées. En se bornant aux résultats, on trouve :
TABLEAU XII — Moyenne géométrique des λm en microns, avec les températures mesurées.
Couple
C = 9 |
n
|
n′
|
√(λ × λ′)
(µm) |
Couple
C = 8 |
n
|
n′
|
√(λ × λ′)
(µm) |
| Mercure - Pluton |
9 |
0 |
22 |
Vénus - Pluton |
8 |
0 |
27,2 |
| Vénus - Neptune |
8 |
1 |
24,4 |
Terre - Neptune |
7 |
1 |
26,4 |
| Terre - Uranus |
7 |
2 |
26,4 |
Mars - Uranus |
6 |
2 |
27,6 |
| Mars - Saturne |
6 |
3 |
19,8 |
Cérès - Saturne |
5 |
3 |
23,2 |
| Cérès - Jupiter |
5 |
4 |
20 |
Jupiter |
4 |
22 |
Une marge d’incertitude de 4 % ne change rien au sens de ces résultats : pour ces couples planétaires, les moyennes géométriques des λm occupent les longueurs de 20 à 28 microns correspondant aux distances de 14,51 à 17,2 UA où le rapport λm / f3 n’excède pas 2.
TABLEAU XIII — Valeurs calculées de la longueur d’onde maximale (λm) et de la force centrale pour trois distances en UA où le rapport λm / f3 est inférieur à 2.
Distance
(UA) |
λm
(µm) |
f3
(µm) |
λm / f3 |
| 14,5 |
28,1 |
28,1 |
1 |
| 15,7 |
29,2 |
24 |
1,22 |
| 17,2 |
30,5 |
20 |
1,52 |
La valeur f3 de l’accélération est fonction de la masse du Soleil et de l’inverse, à la puissance 2, de la distance de l’astre. La λm, à cette distance, est fonction, du rayon du Soleil à la puissance 2, de sa température à la puissance quatrième, de l’albédo de la planète, et de la racine de sa distance au Soleil. En éliminant la distance, paramètre commun, en négligeant le rapport des constantes de Wien et de la gravitation, il reste le rayon du Soleil, sa masse (volume × densité), sa température, à réunir dans une même formule pour comprendre la relation Soleil-planètes et l’équilibre gravité-rayonnement.
Article suivant — 1.6. Modèles solaires
[1] Berkeley : Cours de physique. Armand Collin, 1976.
Atomistique. Hubert Gié. Éd. J.-B. Baillière et Fils, 1967.
Physique atomique. E. Chpolski. Éd. de Moscou, 1967.
Dictionnaire de physique. Jean-Paul Mathieu, Alfred Kastler, Pierre Fleury. Éd. Masson. Eyrolles, 1983.
[2] Les planètes. Georges Bruhat, Evry Schatzman. P.U.F., 1952.