Demi-grands axes et gravités
Il y a de fortes chances pour que le rayon d’une planète résume l’histoire d’un équilibre conquis entre des forces antagonistes de cohésion et de rupture. Puisque l’organisation des orbites principales montre que les demi-grands axes ont subi des règles discriminatoires, on prend peu de risque à les étendre aux rayons stables des planètes du système solaire. On en prend un plus grand à les lier aux distances moyennes. Cela reviendrait à dire que la dimension d’une perle dans son chaton n’est pas indifférente à celle de la bague. La relation est perçue de façon qualitative. Celle qui se propose avec les planètes-perles et les orbites-anneaux est quantitative. Comment varie, et de combien varie le rayon de la perle, quand varie le rayon de l’anneau… et faut-il introduire un autre critère, la masse, pour fonder cette relation ? Question posée aux Céphéides.
Entre la stabilité et l’instabilité, une Céphéide est une étoile pulsante variable. Ce type d’étoile géante (classes F et G comme le Soleil) qui doit son appellation à δ Céphée, l’une de ses premières représentantes, varie suivant une période précise, en magnitude apparente, température, vitesse radiale, intensité, déplacement des raies spectrales, dimension du rayon. Les valeurs des périodes très différentes s’échelonnent de 24 heures à quelques dizaines de jours.
Ces particularités, expliquent Moroz, Bakouline, et Kononovitch, “traduisent le fait que les atmosphères des Céphéides subissent des pulsations régulières. Par conséquent, les conditions qui y règnent sont susceptibles de maintenir pendant longtemps à un niveau constant un processus oscillatoire caractéristique.” Les causes ? Gravité, hydrogène et température :
“… les propriétés les plus importantes d’une étoile sont déterminées par sa structure interne. En particulier, nous avons montré que la ‘combustion’ de l’hydrogène au sein des géantes rouges forme un noyau d’hélium. La contraction gravitationnelle du noyau entraîne l’élévation de la température, l’augmentation de la densité, et, par conséquent, de la pression. Il en résulte que l’étoile se gonfle, comme on l’observe dans les géantes ordinaires. Toutefois, si la pression augmente brusquement, l’étoile passe par inertie par la position d’équilibre et sa dilatation atteint une valeur à laquelle la pression dans le noyau devient plus faible que dans l’enveloppe. Telle est l’origine de la fluctuation des Céphéides. Pour les maintenir, l’apport de l’énergie doit être constant, analogue à la poussée d’un pendule dans une horloge.” [1] Un vulgarisateur des étoiles pulsantes, Dominique Lesueur, en appelle aussi au pendule pour être bien compris : “Les étoiles variables quasi-périodiques, les variables périodiques et les irrégulières sont donc des étoiles pulsantes. Elles sont appelées ainsi parce que leur diamètre change continuellement et cycliquement pendant que sont décrites les périodes successives de la courbe de lumière qui les caractérise. L’étoile se contracte et se dilate alternativement, comme si elle était à la recherche d’une position d’équilibre sans parvenir à la trouver. Ces oscillations successives peuvent être très bien comprises si l’étoile est comparée à un pendule. Si un tel pendule est lâché dans une position autre que sa position d’équilibre (la verticale) il y revient immédiatement mais la dépasse à cause de sa vitesse. Lorsqu’il atteint une position symétrique de celle ou il a été lâché, sa vitesse s’annule et il repart en sens inverse pour une nouvelle oscillation. De même, le diamètre d’une étoile pulsante oscille lui aussi entre deux valeurs maximum et minimum, symétriques par rapport à la position d’équilibre qu’elle garderait si les oscillations n’existaient pas.” [2]
Le pendule revient dans l’exposé savant de docteurs ès sciences physico-mathématiques : “Dans le cas le plus simple des pulsations d’une sphère homogène la période des oscillations Π3 est liée à la densité moyenne de la sphère ρ3 par la relation :”

(avec ρ3 en kg ⋅ m−3)
“ Il est curieux que cette expression se déduit de la formule connue des oscillations d’un pendule, si au lieu de la longueur l’on y porte le rayon de l’étoile et si l’on tient compte de l’accélération de la pesanteur à la surface de l’étoile :”

De cet extrait d’un ouvrage d’éminents professeurs, je ne vous communique que la formule Π3 approchée. Je souligne le commentaire sur la formule du pendule en raison de l’application que j’en ai faite et des insultes qu’elle m’a valu de la part d’un astronome spécimen commun du fanatisme anti-astrologique.
En 1972, pour classer les planètes suivant leur lien avec le Soleil et un critère qui n’est propre qu’à l’astre, j’ai posé le quotient L / g, où L = demi-grand axe, g = intensité de la gravité à la surface. Pourquoi à la surface !… écume l’astromètre, et pas à l’altitude d’un satellite, voire à la hauteur de la Lune ? Parce qu’un astrologue ne raisonne pas en extra-terrestre. Parce que les effets astrologiques concernent des êtres vivants à la surface de la Terre et non des êtres satellisés. Parce qu’il s’agit de savoir s’il existe ou non un lien entre les orbites et les rayons et que ce sont eux, (avec la densité moyenne de l’astre), qui donnent la gravité à la surface.
Le pendule de Foucault est lié à la terre ferme (à la surface !) par un support matériel exclu de la méditation d’Hubert Reeves sur l’action de l’univers. Le rapport L / g, multiplié par 4π2 pour le calcul de la période d’un pendule simple, n’a aucun support. Il constitue un “oscillateur harmonique” abstrait, sans Panthéon, ficelle, tension, ni température. Un pendule purement mathématique… et un moyen de demander aux mathématiques si elles ont une réalité indépendante des accessoires pour sciences expérimentales.
Pour un battement de faible amplitude d’un pendule ou oscillateur simple dont on veut calculer la période Tg, le quotient L / g se change en :

Sachant que g moyen à la surface, s’obtient par le produit rayon × masse volumique r ⋅ ρ :

On écrit en unités terrestres :

La période Tg au carré est proportionnelle au rapport L / r divisé par la masse volumique ρ de l’astre (5,52 g/cm3 = 1 en unité terrestre). La formule groupe 3 variables réputées indépendantes ; l’une d’elle, le demi-grand axe, désigné par L appartenant à un ensemble dont nous connaissons déjà la cohérence. Pour le reste et la suite, malgré l’autorité des docteurs ès sciences précédemment cités, les prudents échangeront le pendule contre un oscillateur harmonique de la même famille (Céphéides, système masse-ressort) de pulsation ωg, en radian ou degré, telle que :

Dans le tableau XXII des rapports L̄ / (r̄ ⋅ ρ̄) et inverses l’unité des masses volumiques est celle de la Terre : 1 = 5,52 g/cm3. Les distances L̄ sont en UA, les rayons moyens en rayon moyen terrestre (6 370 km). Pour le Soleil, L̄ = 5,32 UA, moyenne géométrique des demi-grands axes, couplés de Vénus à Pluton. Pour la Lune, L̄ = distance Terre-Lune en UA. Les planètes doubles Pluton-Chiron et Terre-Lune appellent probablement une formule plus complexe.
TABLEAU XXI — Calcul de ḡ = r̄ ⋅ ρ̄ (gravité moyenne d’une planète à sa surface).
| Planète |
densité ρ̄
(l = 1) |
rayon r̄
(l = 1) |
ḡ = r̄ ⋅ ρ̄
(l = 1) |
| Soleil |
0,255 |
109,3 |
27,87 |
| Vénus |
0,95 |
0,95 |
0,90 |
| Mercure |
0,986 |
0,38 |
0,38 |
| |
| Jupiter |
0,24 |
11,19 |
2,69 |
| Mars |
0,716 |
0,53 |
0,38 |
| Saturne |
0,125 |
9,45 |
1,18 |
| |
| Uranus |
0,234 |
4 |
0,94 |
| Neptune |
0,3 |
3,89 |
1,16 |
| Pluton |
0,38 |
0,18 |
0,068 |
| |
| Lune |
0,605 |
0,27 |
0,16 |
| Terre |
1 |
1 |
1 |
| Cérès |
0,38 |
0,08 |
0,03 |
Avec : ρ̄ = ρ / ρl, r̄ = r / rl, ḡ = g / gl.
TABLEAU XXII — Calcul du rapport L̄ / ḡ pour chaque planète, racine de ce rapport et racine du rapport inverse.
| Planète |
L̄
(l = 1) |
L̄ / ḡ
(l = 1) |
√(L̄ / ḡ)
(l = 1) |
√(ḡ / L̄)
(l = 1) |
| Soleil |
5,32 |
0,191 |
0,437 |
2,288 |
| Vénus |
0,723 |
0,802 |
0,895 |
1,117 |
| Mercure |
0,387 |
1,029 |
1,015 |
0,986 |
| |
| Jupiter |
5,202 |
1,934 |
1,39 |
0,719 |
| Mars |
1,523 |
4 |
2 |
0,5 |
| Saturne |
9,554 |
8,1 |
2,846 |
0,351 |
| |
| Uranus |
19,218 |
20,44 |
4,53 |
0,221 |
| Neptune |
30,109 |
25,96 |
5,09 |
0,196 |
| Pluton |
39,438 |
580,2 |
24 |
0,04 |
| |
| Lune |
1/385 |
0,016 |
0,126 |
7,9 |
| Terre |
1 |
1 |
1 |
1 |
| Cérès |
2,77 |
93,46 |
9,67 |
0,103 |
Avec : L̄ = L / Ll.
La racine de L̄ / ḡ est proportionnelle à la période Tg d’un oscillateur harmonique simple, la racine de son inverse, ḡ / L̄, à la pulsation ωg de l’oscillateur. Si l’on veut transformer les résultats en unités SI il suffit de multiplier L̄ / ḡ de chaque planète par 1,529 × 1010, quotient du demi-grand axe de la Terre, Ll = 1,495 98 × 1011 m, et de gl moyen = 9,81 m/s2.
Les valeurs approchées de la dernière colonne s’obtiennent par les formules empiriques :
| de Soleil à Mars : |
 |
| de Mars à Pluton : |
 |
Le coefficient des sinus est l’inverse de celui des cosinus et les angles Ân communs aux deux formules sont, en degrés : 90° ; 45° ; 40° ; 20,5° ; 0°.
TABLEAU XXIII — Application des deux formules et comparaison avec les données.
| Planète |
angle Ân
(°) |
cos Ân
|
2,3 − 1,7 × cos Ân
|
√(ḡ / L̄)
(l = 1) |
| Soleil |
90 |
0 |
2,3 |
2,288 |
| Vénus |
45 |
0,707 |
1,098 |
1,117 |
| Mercure |
40 |
0,766 |
0,998 |
0,986 |
| Jupiter |
20,5 |
0,937 |
0,708 |
0,719 |
| Mars |
0 |
1 |
0,6 |
0,5 |
| Planète |
angle Ân
(°) |
sin Ân
|
0,5 − 0,44 × sin Ân
|
√(ḡ / L̄)
(l = 1) |
| Mars |
0 |
0 |
0,5 |
0,5 |
| Saturne |
20,5 |
0,35 |
0,348 |
0,351 |
| Uranus |
40 |
0,643 |
0,221 |
0,221 |
| Neptune |
45 |
0,707 |
0,193 |
0,196 |
| Pluton |
90 |
1 |
0,065 |
0,04 |
En raison des erreurs de mesure possibles sur les rayons des planètes gazeuses, ainsi que sur leurs densités, on ne peut pas espérer, pour le moment, améliorer une incertitude de l’ordre de 4 % (sans les racines !). En attendant l’analyse des variantes en fonction des rayons et distances, les moyennes utilisées pour ces premiers résultats reproduisent dans des marges correctes les couples du R.E.T. ainsi que sa division binaire à partir de Mars, son centre de symétrie. Une restitution donnée par les angles Ân, leurs sinus et cosinus.
La réunion des deux formules se représente géométriquement par le quadrant d’une ellipse de 0,44 pour le demi-petit axe (b) et de 1,7 pour le demi-grand axe (a).
Une droite ou un segment de droite est une figure plus simple qu’un quadrant d’ellipse. En désignant par X les √(L̄ / ḡ) des planètes Vénus, Mercure, Jupiter, et par Y celles de Saturne, Uranus, Neptune, sans passer par les angles, la fonction linéaire :

réunit les mêmes couples avec le rapport Soleil/Mars, sensiblement égal au coefficient 4,6 selon le tableau XXII (colonne des √(L̄ / ḡ) : 2 / 0,437 = 4,58). Application de la formule :
TABLEAU XXIV — Calcul des X = √(L̄ / ḡ) par Y = 4,6 × (2 − X)
| Planète |
X =
√(L̄ / ḡ) |
Planète |
Y =
√(L̄ / ḡ) |
4,6 × (2 − X)
|
| Vénus |
0,895 |
Neptune |
5,09 |
5,083 |
| Mercure |
1,015 |
Uranus |
4,53 |
4,53 |
| Jupiter |
1,39 |
Saturne |
2,846 |
2,806 |
| Mars |
2 |
|
0 |
0 |
Que l’on soit ou non favorable à l’astrologie et à la démarche qui conduit à cette relation, sa précision suffit à convaincre d’une organisation du système solaire par une répartition symétrique des rapports L / g des planètes principales. Cet essai de cosmogonie astrologique pourrait s’arrêter là… et un esprit qui ne mesure que par de grandes lignes (la droite est indiquée) jugera la suite superflue.
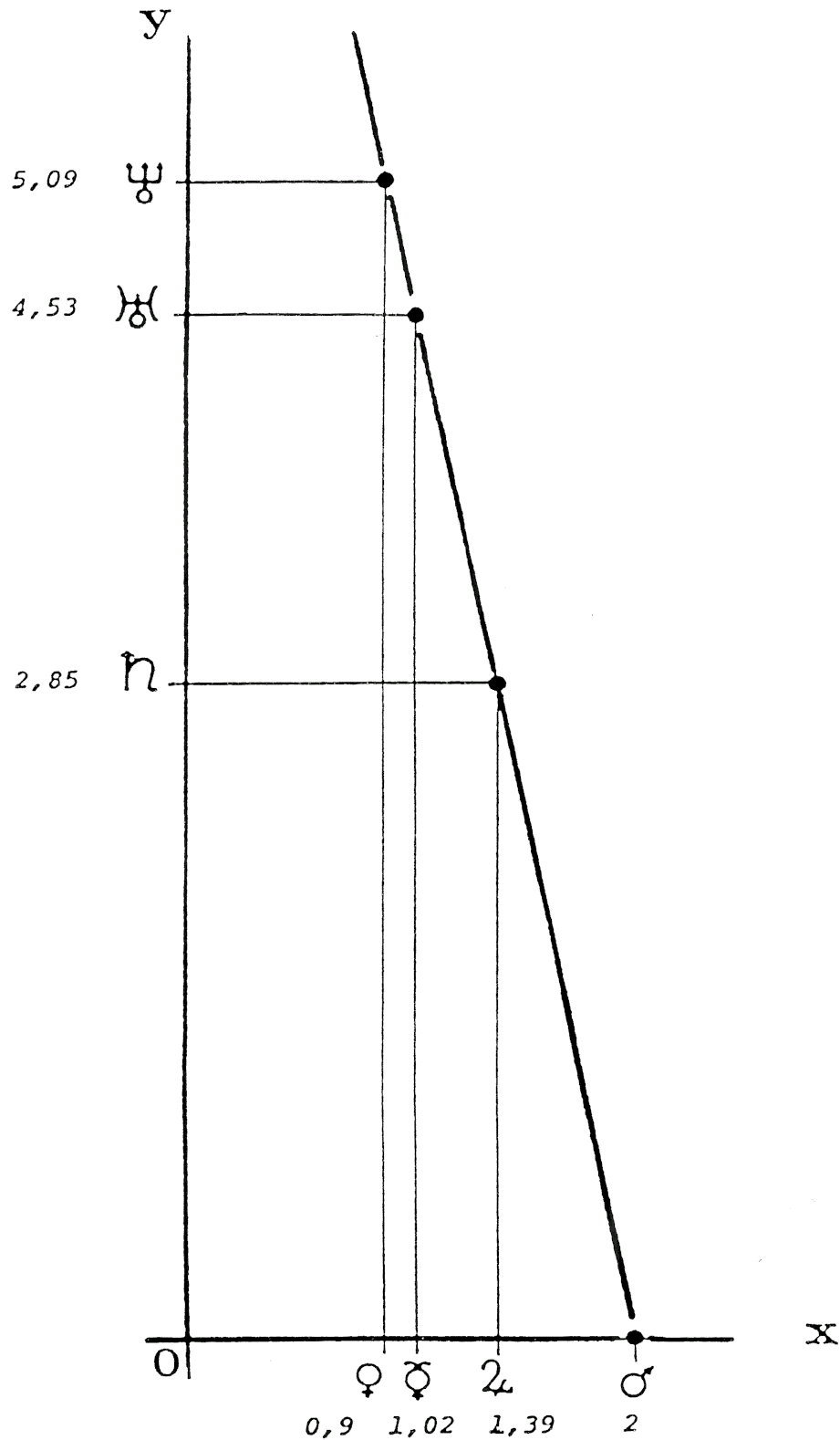
FIG. 15 — Les rapports arrondis de √(L̄ / ḡ) pour les planètes Vénus, Mercure, Jupiter, Mars sont portés en X, sur l’axe des abscisses. Les ordonnées Y, obtenues par la formule Y = 4,6 × (2 − X), restituent à moins de 2 % d’erreur relative les données moyennes mesurées (expérimentales) de Saturne. Uranus, Neptune qui se trouvent ainsi couplées conformément aux prévisions théoriques du modèle R.E.T.
Article suivant — 2.3. D’oscillations en translations
[1] Astronomie. M. Dagaev, V. Demine, I. Klimichine, V. Tcharouguine. Éd. Mir. Moscou, 1986.
[2] Les étoiles pulsantes. Ciel et Espace n° 173, 1980.